题目内容
设函数f(x)=sin(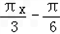 )﹣
)﹣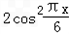 .
.
(1)求f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
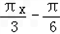 )﹣
)﹣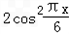 .
.(1)求f(x)的最小正周期及单调递增区间;
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,求当x∈[0,1]时,函数y=g(x)的最大值.
解:(1)函数f(x)=sin(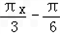 )﹣
)﹣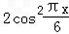
=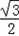 sin
sin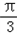 x﹣
x﹣ cos
cos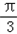 x﹣1
x﹣1
=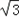 sin(
sin(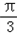 x﹣
x﹣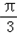 )﹣1,
)﹣1,
故f(x)的最小正周期为 =6.
=6.
由 2kπ﹣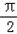 ≤
≤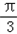 x﹣
x﹣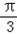 ≤2kπ+
≤2kπ+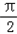 ,k∈z,解得 6k﹣
,k∈z,解得 6k﹣ ≤x≤6k+
≤x≤6k+ ,
,
故单调递增区间为[6k﹣ ,6k+
,6k+ ],k∈z.
],k∈z.
(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,
故当x∈[0,1]时,函数y=g(x)的最大值,即为x∈[3,4]时,函数y=f(x)的最大值.
此时,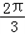 ≤
≤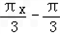 ≤π,0≤sin(
≤π,0≤sin(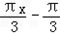 )≤
)≤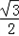 ,﹣1≤f(x)≤
,﹣1≤f(x)≤ ,
,
故函数y=f(x)的最大值为 .
.
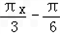 )﹣
)﹣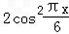
=
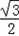 sin
sin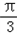 x﹣
x﹣ cos
cos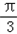 x﹣1
x﹣1=
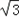 sin(
sin(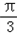 x﹣
x﹣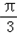 )﹣1,
)﹣1,故f(x)的最小正周期为
 =6.
=6.由 2kπ﹣
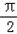 ≤
≤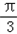 x﹣
x﹣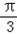 ≤2kπ+
≤2kπ+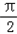 ,k∈z,解得 6k﹣
,k∈z,解得 6k﹣ ≤x≤6k+
≤x≤6k+ ,
,故单调递增区间为[6k﹣
 ,6k+
,6k+ ],k∈z.
],k∈z.(2)若函数y=g(x)与y=f(x)的图象关于直线x=2对称,
故当x∈[0,1]时,函数y=g(x)的最大值,即为x∈[3,4]时,函数y=f(x)的最大值.
此时,
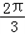 ≤
≤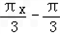 ≤π,0≤sin(
≤π,0≤sin(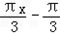 )≤
)≤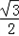 ,﹣1≤f(x)≤
,﹣1≤f(x)≤ ,
,故函数y=f(x)的最大值为
 .
.
练习册系列答案
相关题目