题目内容
三个学校分别有1名、2名、3名学生获奖,这6名学生排成一排合影,要求同校的任2名学生不能相邻,那么不同的排法有 ( )A.36种 B.72种 C.108种 D.120种
答案:D 【解析】本题考查排列组合综合应用;设学生A在甲学校,学生B、C在乙学校,学生D、E、F在丙学校,分两类:(一)学生A与B、C不相邻,首先安排D、E、F,有![]() 种方法,D、E、F之间有四个空位,将A、B、C插入有2
种方法,D、E、F之间有四个空位,将A、B、C插入有2![]() 种方法,所以共有2
种方法,所以共有2![]()
![]() =72种
=72种
方法;(二)学生A与B、C之一相邻,有![]() =48种方法;∴不同排法种数共有72+48=120种.
=48种方法;∴不同排法种数共有72+48=120种.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 B.
B. C.
C. D.
D.
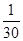 B.
B.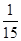 C.
C.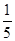 D.
D.