题目内容
已知圆M∶![]() 与圆N∶
与圆N∶![]() 2x+2y-2=0交于A、B两点,且这两点平分圆N的圆周.求圆M的圆心轨迹方程,并求其中半径最小时圆M的方程.
2x+2y-2=0交于A、B两点,且这两点平分圆N的圆周.求圆M的圆心轨迹方程,并求其中半径最小时圆M的方程.
答案:
解析:
解析:
|
两圆方程相减,得公共弦AB所在直线方程: 2(m+1)x+2(n+1)y- 由条件,直线过N的圆心(-1,-1), ∴ 即 即圆M的圆心轨迹方程为 又圆M的方程为 ∴半径r= 可求得n=-2时m=-1,此时不等式取等号, 即半径r取最小值 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足 )2+y2=
)2+y2=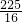 的圆心为M,圆N:(x-
的圆心为M,圆N:(x- )2+y2=
)2+y2= 的圆心为M,圆N:(x-
的圆心为M,圆N:(x- )2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.
)2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.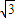 )2+y2=
)2+y2=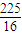 的圆心为M,圆N:(x-
的圆心为M,圆N:(x-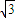 )2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.
)2+y2=的圆心为N,一动圆与圆M内切,与圆N外切.