题目内容
已知圆M：（x+
）2+y2=
的圆心为M，圆N：（x-
）2+y2=的圆心为N，一动圆与圆M内切，与圆N外切．（Ⅰ）求动圆圆心P的轨迹方程；
（Ⅱ）在（Ⅰ）所求轨迹上是否存在一点Q，使得∠MQN为钝角？若存在，求出点Q横坐标的取值范围；若不存在，说明理由．
【答案】分析：（I）根据动圆与圆M内切，与圆N外切，得出则
，从而有根据|PM|+|PN|=4＞|MN|，椭圆的定义可得P点的轨迹是以M，N为焦点的椭圆，求出a、b的值，即得椭圆的标准方程．
（II）先假设存在一点Q，并设Q（x，y），从而得出
，然后与椭圆方程联立并化简得出
，即可得出结果．
解答：解：（Ⅰ）设动圆P的半径为r，则
两式相加得|PM|+|PN|=4＞|MN|
由椭圆定义知，点P的轨迹是以M、N为焦点，焦距为
，实轴长为4的椭圆
其方程为
…（6分）
（Ⅱ）假设存在，设Q（x，y）．则因为∠MQN为钝角，所以
，
，
又因为Q点在椭圆上，所以
联立两式得：
化简得：
，
解得：
，所以存在．…（13分）
点评：本题考查圆与圆的位置关系，椭圆的定义和标准方程，得到|PM|+|PN|=4＞|MN|是解题的关键．
，从而有根据|PM|+|PN|=4＞|MN|，椭圆的定义可得P点的轨迹是以M，N为焦点的椭圆，求出a、b的值，即得椭圆的标准方程．（II）先假设存在一点Q，并设Q（x，y），从而得出
，然后与椭圆方程联立并化简得出，即可得出结果．解答：解：（Ⅰ）设动圆P的半径为r，则
两式相加得|PM|+|PN|=4＞|MN|
由椭圆定义知，点P的轨迹是以M、N为焦点，焦距为
，实轴长为4的椭圆其方程为
…（6分）（Ⅱ）假设存在，设Q（x，y）．则因为∠MQN为钝角，所以
，，又因为Q点在椭圆上，所以
联立两式得：
化简得：，解得：
，所以存在．…（13分）点评：本题考查圆与圆的位置关系，椭圆的定义和标准方程，得到|PM|+|PN|=4＞|MN|是解题的关键．
练习册系列答案
相关题目
）2+y2=
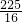的圆心为M，圆N：（x-
）2+y2=36，定点N（
，0），点P为圆M上的动点，点Q在NP上，点G在MP上，且满足
。
是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由。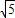
）2+y2=36，定点N（
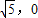），点P为圆M上的动点，点G在MP上，且满足|GP|=|GN|
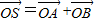，是否存在这样的直线l，使四边形OASB的对角线相等（即|OS|=|AB|）？若存在，求出直线l的方程；若不存在，试说明理由．
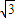）2+y2=
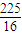的圆心为M，圆N：（x-
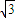）2+y2=的圆心为N，一动圆与圆M内切，与圆N外切．
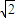）2+y2=r2=r2（r＞0）．若椭圆C：
+
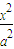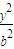=1（a＞b＞0）的右顶点为圆M的圆心，离心率为
．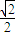