题目内容
(本小题满分12分)
设函数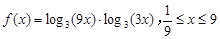 .
.
(Ⅰ)若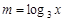 ,求
,求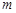 取值范围;
取值范围;
(Ⅱ)求 的最值,并给出最值时对应的
的最值,并给出最值时对应的 的值.
的值.
(1)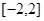 (2)
(2)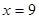 时
时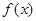 取得最大值
取得最大值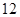
解析试题分析:解:(Ⅰ)∵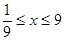 ,
,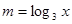 为增函数,
为增函数,
∴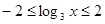 ,即
,即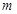 取值范围是
取值范围是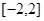 …………………4分
…………………4分
(Ⅱ)由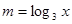 得:
得:
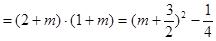 , ………………………6分
, ………………………6分
又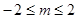 ,∴当
,∴当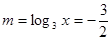 ,即
,即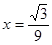 时
时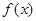 取得最小值
取得最小值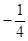 , ………9分
, ………9分
当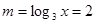 ,即
,即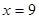 时
时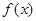 取得最大值
取得最大值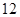 . ………………………12分
. ………………………12分
考点:本试题考查了对数函数的性质。
点评:解决该试题的关键是对于对数函数的性质的熟练 运用,以及构造变量,得到形如二次函数,结合二次函数的性质求解得到,属于中档题。

练习册系列答案
相关题目
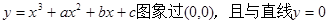 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为 ;
;
 ,当
,当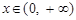 时,有
时,有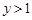 ,解关于x的不等式
,解关于x的不等式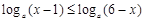
 ,设AB=2x,BC=y.
,设AB=2x,BC=y.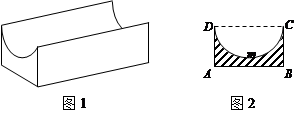
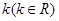 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点. 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为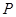 元,且
元,且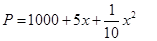 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为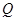 元,其中
元,其中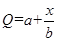
 ,
,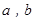 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)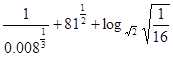 ;
;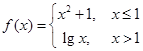 ,则
,则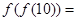 _______________.
_______________.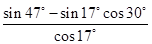 =____________.
=____________.