题目内容
四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形,
 则直线
则直线 与底面
与底面 的关系是( )
的关系是( )
| A.平行 | B.垂直 |
| C.在平面内 | D.成60°角 |
B
解析试题分析:∵ ∴
∴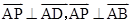 又∵AB∩AD=A∴
又∵AB∩AD=A∴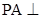 平面ABCD.
平面ABCD.
考点:1.空间向量的坐标运算;2.线面垂直的判定定理.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
已知向量 ,
, ,
, ,若
,若 ,则k =( )
,则k =( )
| A.1 | B.3 | C.5 | D.7 |
以下四组向量:① ,
, ;②
;② ,
, ;③
;③ ,
, ;④
;④ ,
,
其中互相平行的是.
| A.②③ | B.①④ | C.①②④ | D.①②③④ |
已知点 ,若向量
,若向量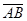 与
与 同向,且
同向,且 ,则点
,则点 的坐标为( )
的坐标为( )
A. | B. | C. | D. |
设向量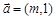 ,
,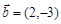 ,若满足
,若满足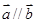 ,则
,则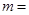 ( )
( )
A.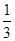 | B.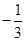 | C.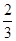 | D.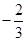 |
若非零向量 满足
满足 //
// ,且
,且 ,则
,则 ( )
( )
| A.4 | B.3 | C.2 | D.0 |
已知 外接圆的半径为1,圆心为O.若
外接圆的半径为1,圆心为O.若 ,且
,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D.3 |
已知向量a=(-1,2),则下列向量与a共线的是( )
| A.b=(1,-2) | B.b=(2,-1) |
| C.b=(0,1) | D.b="(1,1)" |
 :
: ,若存在过右焦点
,若存在过右焦点 的直线与双曲线
的直线与双曲线 两点且
两点且 ,则双曲线离心率的最小值为( )
,则双曲线离心率的最小值为( )


