题目内容
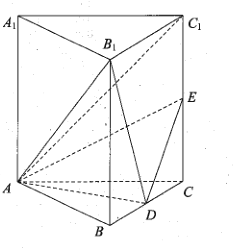
【题目】如图，直三棱柱
中，
，
，
分别是
的中点．
（1）证明：平面
平面
；
（2）求三棱锥
的高．
【答案】(1)证明见解析；(2)1.
【解析】分析：（1）要证明平面
平面
，利用平面与平面垂直的判定定理，在其中一个平面内找一条直线与另一个平面垂直。由
，
是
的中点，可得
。因为三棱柱
为直三棱柱，所以
平面
，进而可得
。由已知条件直三棱柱中，
，
，
分别是
的中点．可得：
，进而得
∽
，所以
，所以
。因为
，由直线与平面垂直的判定定理可得
平面，再由平面与平面垂直的判定定理可得平面平面。（2）求三棱锥
的高，直接作高不容易判断垂足的位置，故可以用等体积法求高。由（1）可知可用 
来求。由（1）知直线平面ADE，故求
，
,，进而求得
。由条件可求得
， 
，知三角形边长要求面积，应先求一个角，故由余弦定理推论可得：
，进而求
，可求
, 设三棱锥的高为
，由，得：
，解得
.
详解：（1）由已知得：
所以∽
所以，所以
又因为，是的中点，所以
所以平面，所以
而，所以平面
又
平面
，
所以平面平面；
（2）设三棱锥的高为，因为
,
所以，
由已知可求得， ，
在
中，由余弦定理的推论可得 ，
所以，所以,
由，得：，所以.
练习册系列答案
相关题目
【题目】某地煤气公司规定，居民每个月使用的煤气费由基本月租费、保险费和超额费组成．每个月的保险费为3元，当每个月使用的煤气量不超过am3时，只缴纳基本月租费c元；如果超过这个使用量，超出的部分按b元/m3计费．
（1）请写出每个月的煤气费y（元）关于该月使用的煤气量x（m3）的函数解析式；
（2）如果某个居民7～9月份使用煤气与收费情况如下表，请求出a，b，c，并画出函数图象；
月份 | 煤气使用量/m3 | 煤气费/元 |
7 | 4 | 4 |
8 | 10 | 10 |
9 | 16 | 19 |
其中，仅7月份煤气使用量未超过am3．
