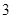题目内容
设P是双曲线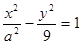 上一点,该双曲线的一条渐近线方程是
上一点,该双曲线的一条渐近线方程是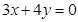 ,
,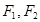 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若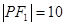 ,则
,则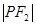 等于 ( )
等于 ( )
| A.2 | B.18 | C.2或18 | D.16 |
C
解析试题分析:因为双曲线 渐近线方程是
渐近线方程是 ,所以
,所以 又因为
又因为 ,所以
,所以 等于2或18
等于2或18
考点:双曲线定义,渐近线方程

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
双曲线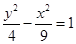 的渐近线的方程是( )
的渐近线的方程是( )
A.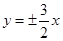 | B. | C.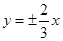 | D.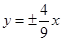 |
设 为抛物线
为抛物线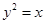 上的动弦,且
上的动弦,且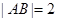 , 则弦
, 则弦 的中点
的中点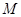 到
到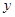 轴的最小距离为
轴的最小距离为
| A.2 | B.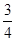 | C.1 | D.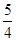 |
已知椭圆 上一点
上一点 到右焦点的距离是1,则点
到右焦点的距离是1,则点 到左焦点的距离是( )
到左焦点的距离是( )
A. | B. | C. | D. |
已知双曲线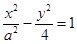 的右焦点与抛物线y2=12x的焦点重合,则该双曲线的离心率等于
的右焦点与抛物线y2=12x的焦点重合,则该双曲线的离心率等于
A.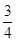 | B.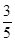 | C.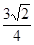 | D.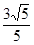 |
已知椭圆E: =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
A. =1 =1 | B.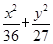 =1 =1 | C.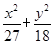 =1 =1 | D. =1 =1 |
已知椭圆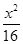 +
+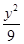 =1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
=1及以下3个函数:①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函数图像能等分该椭圆面积的函数个数有( )
| A.1个 | B.2个 |
| C.3个 | D.0个 |
已知点F1,F2是双曲线 =1(a>0,b>0)的左、右焦点,点P是双曲线上的一点,且
=1(a>0,b>0)的左、右焦点,点P是双曲线上的一点,且 =0,则△PF1F2的面积为( )
=0,则△PF1F2的面积为( )
| A.ab | B.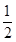 ab ab | C.b2 | D.a2 |
 的焦点
的焦点 与双曲
与双曲 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与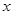 轴的交点为
轴的交点为 ,点
,点 在抛物线上且
在抛物线上且 ,则
,则