题目内容
过椭圆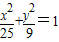 的中心的直线与椭圆交于A、B两点,F1是椭圆的右焦点,则△ABF1的面积的最大值为 .
的中心的直线与椭圆交于A、B两点,F1是椭圆的右焦点,则△ABF1的面积的最大值为 .
【答案】分析:当AB⊥x轴时,AB为椭圆的短轴,可得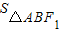 =
=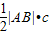 .
.
当AB与x轴不垂直时,设直线AB:y=kx,(k≠0),联立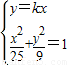 ,可得点A,B的坐标.利用
,可得点A,B的坐标.利用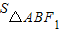 =
=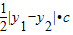 即可得出.
即可得出.
解答:解:由椭圆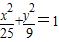 ,可得a2=25,b2=9,∴
,可得a2=25,b2=9,∴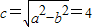 .
.
①当AB⊥x轴时,AB为椭圆的短轴,∴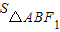 =
=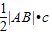 =
=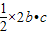 =3×4=12.
=3×4=12.
②当AB与x轴不垂直时,设直线AB:y=kx,(k≠0),
联立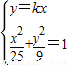 ,化为(9+25k2)x2=225,
,化为(9+25k2)x2=225,
解得x=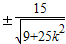 .得到y=
.得到y=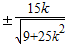 .
.
∴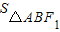 =
=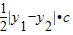 =
=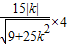 =
=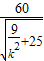
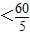 =12.
=12.
综上可知:△ABF1的面积的最大值为12.
点评:熟练掌握直线与椭圆相交问题转化为方程联立得出交点坐标、分类讨论思想方法是解题的关键.
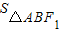 =
=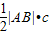 .
.当AB与x轴不垂直时,设直线AB:y=kx,(k≠0),联立
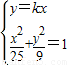 ,可得点A,B的坐标.利用
,可得点A,B的坐标.利用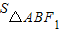 =
=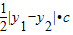 即可得出.
即可得出.解答:解:由椭圆
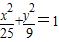 ,可得a2=25,b2=9,∴
,可得a2=25,b2=9,∴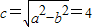 .
.①当AB⊥x轴时,AB为椭圆的短轴,∴
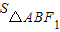 =
=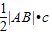 =
=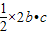 =3×4=12.
=3×4=12.②当AB与x轴不垂直时,设直线AB:y=kx,(k≠0),
联立
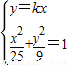 ,化为(9+25k2)x2=225,
,化为(9+25k2)x2=225,解得x=
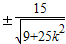 .得到y=
.得到y=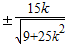 .
.∴
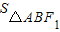 =
=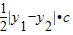 =
=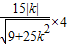 =
=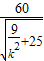
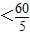 =12.
=12.综上可知:△ABF1的面积的最大值为12.
点评:熟练掌握直线与椭圆相交问题转化为方程联立得出交点坐标、分类讨论思想方法是解题的关键.

练习册系列答案
相关题目
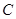 的中心在原点,焦点在
的中心在原点,焦点在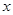 轴上,离心率为
轴上,离心率为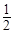 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线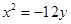 的焦点.
的焦点.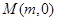 的直线
的直线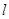 与椭圆
与椭圆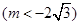 ,直线
,直线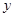 轴交于点
轴交于点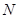 ,当
,当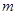 为何值时
为何值时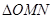 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值. 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
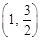 .
. (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 ,由题意得
,由题意得

 ,代入椭圆
,代入椭圆 .
. ,
,
 .解得。
.解得。 .……………………4分
.……………………4分 .
.
 ,
, ,
,
 .
. .
. ,解得
,解得 .
.