题目内容
在极坐标系中,从极点O作直线与另一直线l:ρcosθ=4相交于点M,在OM上取一点P,使OM•OP=12.设R为l上任意一点,则RP的最小值分析:设P(ρ,θ),根据OM•OP=12先求出点P的极坐标方程式,得到其直角坐标方程,最后通过观察图形即可得最小值.
解答: 解:设P(ρ,θ),OM=
解:设P(ρ,θ),OM=
,
∵OM•OP=12.
∴ρ=3cosθ.
故P在圆:x2+y2=32上,
而R为直线l:x=4.
由图象知,RPmin=1.
 解:设P(ρ,θ),OM=
解:设P(ρ,θ),OM=| 4 |
| cosθ |
∵OM•OP=12.
∴ρ=3cosθ.
故P在圆:x2+y2=32上,
而R为直线l:x=4.
由图象知,RPmin=1.
点评:本小题主要考查直线与圆的极坐标方程的有关知识,以及转化与化归的思想方法.解决本题的关键是将它们转化为直角坐标系下的直线与圆的位置关系问题来处理.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
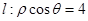 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使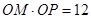 .
.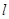 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值.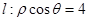 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使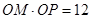 .设R为
.设R为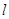 上任意一点,则RP的最小值 .
上任意一点,则RP的最小值 .