题目内容
在极坐标系中,从极点O作直线与另一直线l:ρcosθ=4相交于点M,在OM上取一点P,使
•
=12.
(1)求点P的轨迹方程;(2)设R为l上任意一点,试求RP的最小值.
| OM |
| OP |
(1)求点P的轨迹方程;(2)设R为l上任意一点,试求RP的最小值.
分析:(1)求出直线l的普通方程,设出M的坐标,P的坐标,建立M,P两点的坐标关系,求出向量
,
,通过
•
=12,求出点P的轨迹方程;
(2)要求RP的最小值,就是求圆心到直线的距离减去半径即可.
| OM |
| OP |
| OM |
| OP |
(2)要求RP的最小值,就是求圆心到直线的距离减去半径即可.
解答:解:(1)直线ρcosθ=4在平面直角坐标系中对应的方程为x=4,
设M的坐标 (4,b),P点坐标为(x,y),
则
=
,b=
,
=(4,b),
=(x,y),
∵
•
=12,4x+by=12,
所以4x+
•y=12,x2-3x+y2=0这就是所求圆的方程,化为标准式为(x-
)2+y2=
;
(2)因为R为l上任意一点,(x-
)2+y2=
;
圆心坐标(
,0),半径为:
;
则圆心到直线x=4的距离为:4-
=
,
圆的半径为:
,
所以所求RP的最小值为
-
=1.
设M的坐标 (4,b),P点坐标为(x,y),
则
| b |
| 4 |
| y |
| x |
| 4y |
| x |
| OM |
| OP |
∵
| OM |
| OP |
所以4x+
| 4y |
| x |
| 3 |
| 2 |
| 9 |
| 4 |
(2)因为R为l上任意一点,(x-
| 3 |
| 2 |
| 9 |
| 4 |
圆心坐标(
| 3 |
| 2 |
| 3 |
| 2 |
则圆心到直线x=4的距离为:4-
| 3 |
| 2 |
| 5 |
| 2 |
圆的半径为:
| 3 |
| 2 |
所以所求RP的最小值为
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题是中档题,考查动点的轨迹方程的求法,极坐标与直角坐标方程的转化,两点之间的距离,转化为圆心到直线的距离的求法,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
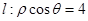 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使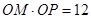 .
.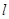 上任意一点,试求RP的最小值.
上任意一点,试求RP的最小值.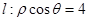 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使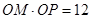 .设R为
.设R为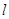 上任意一点,则RP的最小值 .
上任意一点,则RP的最小值 .