题目内容

7．已知a、b、c为△ABC的三边长，且关于x的二次方程x2-2x+lg（c2-b2）-2lga+1=0有等根，试判断△ABC的形状．

分析 关于x的方程x2-2x+lg（c2-b2）-lga2+1=0有等根，可得△=0，化为lg（c2-b2）=lga2，即c2-b2=a2，即可得出．

解答 解：∵关于x的二次方程x2-2x+lg（c2-b2）-2lga+1=0有等根，
即：x2-2x+lg（c2-b2）-lga2+1=0有等根，
∴△=4-4[lg（c2-b2）-lga2+1]=0，
化为lg（c2-b2）=lga2，
∴c2-b2=a2，
即c2=a2+b2．
∴△ABC为直角三角形．

点评 本题考查了一元二次方程有实数根与判别式的关系、对数的运算性质、勾股定理的逆定理，考查了计算能力，属于中档题．

练习册系列答案
相关题目
17．已知函数f（x）=sin（x+$\frac{π}{6}$），将y=f（x）的图象上所有点的横坐标扩大为原来的2倍（纵坐标不变）得到y=h（x）的图象．
（1求y=h（x）的单调递增区间；
（2）若f（α）=$\frac{1}{4}$，求sin（$\frac{5π}{6}$-α）+sin2（$\frac{π}{3}$-α）的值．
18．已知函数f（x）=$\left\{\begin{array}{l}x+2\\{x^2}\\ 2x\end{array}$$\begin{array}{l}（x≤-1），\\（-1＜x＜2），\\（x≥2），\end{array}$如果f（x）=3，那么x的值是（　　）
A．1B．$\sqrt{3}$C．$±\sqrt{3}$D．$\frac{3}{2}$
15．在数字1，2，…，n（n≥2）的任意一个排列A：a1，a2，…，an中，如果对于i，j∈N*，i＜j，有ai＞aj，那么就称（ai，aj）为一个逆序对．记排列A中逆序对的个数为S（A）．
如n=4时，在排列B：3，2，4，1中，逆序对有（3，2），（3，1），（2，1），（4，1），则S（B）=4．
（Ⅰ）设排列 C：3，5，6，4，1，2，写出S（C）的值；
（Ⅱ）对于数字1，2，…，n的一切排列A，求所有S（A）的算术平均值；
（Ⅲ）如果把排列A：a1，a2，…，an中两个数字ai，aj（i＜j）交换位置，而其余数字的位置保持不变，那么就得到一个新的排列A'：b1，b2，…，bn，求证：S（A）+S（A'）为奇数．
2．若直线x=a是函数y=sin（x+$\frac{π}{6}$）图象的一条对称轴，则a的值可以是（　　）
A．$\frac{π}{3}$B．$\frac{π}{2}$C．-$\frac{π}{6}$D．-$\frac{π}{3}$
12．已知抛物线y2=2px（p＞0）过点（4，4），它的焦点F，倾斜角为$\frac{π}{3}$的直线l过点F且与抛物线两交点为A，B，点A在第一象限内．
（1）求抛物线和直线l的方程；
（2）求|AF|=m|BF|，求m的值．
19．①x+$\frac{1}{x}$≥2；②|x+$\frac{1}{x}$|≥2；③$\frac{{x}^{2}+{y}^{2}}{xy}$≥2；④$\frac{{x}^{2}+{y}^{2}}{2}$＞xy；⑤$\frac{|x+y|}{2}$≥$\sqrt{|xy|}$．其中正确的是②（写出序号即可）．
16．已知各项均为正数的数列{an}的前n项和为Sn，且4Sn=a${\;}_{n}^{2}$+2an+1（n∈N*）．
（1）求{an}的通项公式；
（2）设f（n）=$\left\{\begin{array}{l}{{a}_{n}，n=2k-1}\\{f（\frac{n}{2}），n=2k}\end{array}\right.$（n，k∈N*），bn=f（2n+4），求数列{bn}的前n项和Tn．
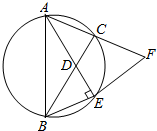17．如图，在△ABC中，∠BAC的平分线交BC于D，交△ABC的外接圆于E，延长AC到F，使得AC•AF=AD•AE，连按EF．
（1）求证：C、D、E、F四点共圆；
（2）求证：AC•DE=EF•CD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网