题目内容
(理科)设x,y∈R,x≥0,y≤0且x2+y2=4,则
ydx=
| ∫ | 2 0 |
-π
-π
.分析:由条件先求出函数y的不等式,利用积分的几何意义求积分即可.
解答:解:∵x≥0,y≤0且x2+y2=4,
∴y=-
,(x≥0),
∴函数y对应的图象为
圆周,对应的面积为S=
•π×22=π.
则根据积分几何意义知
ydx=-S=-π,
故答案为:-π.

∴y=-
| 4-x2 |
∴函数y对应的图象为
| 1 |
| 4 |
| 1 |
| 4 |
则根据积分几何意义知
| ∫ | 2 0 |
故答案为:-π.
点评:本题主要考查定积分的应用,利用积分的几何意义是解决本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 ·
· ,其中
,其中 ,2).
,2). 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R ·
· ,其中
,其中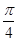 ,2).
,2).