题目内容
定义在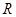 上的函数
上的函数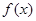 对任意
对任意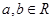 都有
都有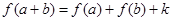 (
(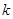 为常数).
为常数).
(1)判断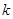 为何值时
为何值时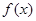 为奇函数,并证明;
为奇函数,并证明;
(2)设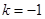 ,
,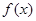 是
是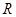 上的增函数,且
上的增函数,且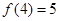 ,若不等式
,若不等式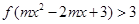 对任意
对任意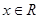 恒成立,求实数
恒成立,求实数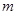 的取值范围.
的取值范围.
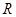 上的函数
上的函数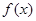 对任意
对任意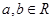 都有
都有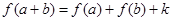 (
(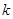 为常数).
为常数).(1)判断
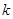 为何值时
为何值时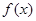 为奇函数,并证明;
为奇函数,并证明;(2)设
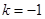 ,
,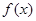 是
是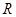 上的增函数,且
上的增函数,且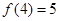 ,若不等式
,若不等式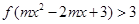 对任意
对任意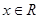 恒成立,求实数
恒成立,求实数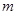 的取值范围.
的取值范围.(1) ,证明过程详见解析;(2)
,证明过程详见解析;(2) .
.
 ,证明过程详见解析;(2)
,证明过程详见解析;(2) .
.试题分析:本题主要考查抽象函数奇偶性的判断和利用函数单调性解不等式.考查学生的分析问题解决问题的能力.考查转化思想和分类讨论思想.第一问,用赋值法证明函数的奇偶性;第二问,利用单调性解不等式,转化成恒成立问题,再利用二次函数的性质求
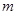 的取值范围.
的取值范围.试题解析:(Ⅰ)若
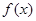 在
在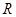 上为奇函数,则
上为奇函数,则 , 1分
, 1分令
 ,则
,则 ,∴
,∴ . 2分
. 2分证明:由
 ,令
,令 ,则
,则 ,
,又
 ,则有
,则有 .即
.即 对任意
对任意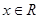 成立,所以
成立,所以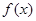 是奇函数.
是奇函数.6分
(Ⅱ)
 7分
7分∴
 对任意
对任意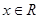 恒成立.
恒成立.又
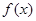 是
是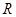 上的增函数,∴
上的增函数,∴ 对任意
对任意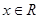 恒成立, 9分
恒成立, 9分即
 对任意
对任意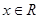 恒成立,
恒成立,当
 时显然成立;
时显然成立;当
 时,由
时,由 得
得 .
.所以实数m的取值范围是
 . 13分
. 13分
练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
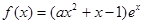 ,其中
,其中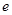 是自然对数的底数,
是自然对数的底数,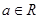 .
.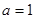 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;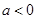 ,求
,求 ,函数
,函数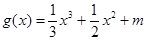 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围. 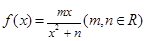 在
在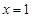 处取得极值
处取得极值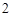 .
.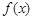 的解析式;
的解析式; 是曲线
是曲线 上除原点
上除原点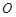 外的任意一点,过
外的任意一点,过 的中点且垂直于
的中点且垂直于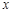 轴的直线交曲线于点
轴的直线交曲线于点 ,试问:是否存在这样的点
,试问:是否存在这样的点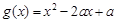 ,若对于任意
,若对于任意 ,总存在
,总存在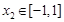 ,使得
,使得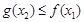 ,求实数
,求实数 的取值范围.
的取值范围. 上的不同三点,O是
上的不同三点,O是 满足
满足 ,记
,记 ;
;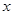 ,使
,使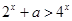 成立,则实数
成立,则实数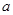 的取值范围是 .
的取值范围是 .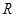 上的函数
上的函数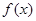 是周期为
是周期为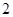 的偶函数,当
的偶函数,当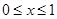 时,
时,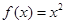 ,如果直线
,如果直线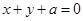 与曲线
与曲线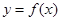 恰有两个交点,则实数
恰有两个交点,则实数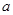 的值是( )
的值是( )
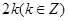
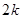 或
或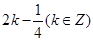
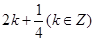
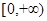 上是增函数,则
上是增函数,则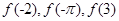 的大小关系是( )
的大小关系是( )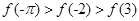
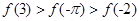
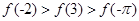
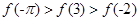
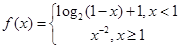 ,若
,若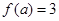 ,则
,则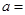 .
. 若
若 则
则 ( )
( )


