题目内容
若非零向量α、β满足|α+β|=|α-β|,则α与β的夹角为_________.

解析一:如图所示,以α、β为邻边作出![]() OACB,则
OACB,则![]() =α+β,
=α+β,![]() =α-β,又|α+β|=|α-β|,即平行四边形OACB的对角线长相等,所以OACB为矩形,所以α⊥β,即它们的夹角为90°.
=α-β,又|α+β|=|α-β|,即平行四边形OACB的对角线长相等,所以OACB为矩形,所以α⊥β,即它们的夹角为90°.
解析二:因为|α+β|=|α-β|,
所以α2+2α·β+β2=α2-2α·β+β2,即α·β=0.
所以α⊥β,即α、β的夹角为90°.
答案:90°
温馨提示
向量问题的几何意义很重要.本题的解法一就是向量运算的几何解法,解法二则运用了向量数量积的代数运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、
、 ,满足
,满足 ,且
,且 ,则
,则 R,
R, ”的否定是“
”的否定是“ ”;
”; ②若
②若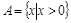 ,
, ,则
,则 ( RB)=A;
( RB)=A; 是偶函数的充要条件是
是偶函数的充要条件是 (
( Z);
Z); b,b=
b,b= R),则
R),则 .
. 、
、 ,满足
,满足 ,且
,且 ,则
,则 与
与 的夹角大小为 .
的夹角大小为 .