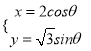题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的最值;
上的最值;
(2)若![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最大值(参考数据:
的最大值(参考数据:![]() )
)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求出函数的导函数,求出函数的单调性从而求得函数的最值;
(2)依题意可得![]() 对任意
对任意![]() 恒成立,参变分离可得
恒成立,参变分离可得![]() 对任意
对任意![]() 恒成立.令
恒成立.令![]() 利用导数说明其单调性,求出函数的最小值,即可求出参数的取值范围;
利用导数说明其单调性,求出函数的最小值,即可求出参数的取值范围;
解:(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,显然
,显然![]() ,
,
所以![]() ,
,![]() .
.
(2)因为![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
由于![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,
![]() .
.
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() .
.
又![]() ,即
,即![]() ,所以
,所以![]() .
.
所以![]() .
.
因为![]() ,所以
,所以![]()
又因为![]() 对任意
对任意![]() 恒成立,所以
恒成立,所以![]() .
.
又![]() ,所以
,所以![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
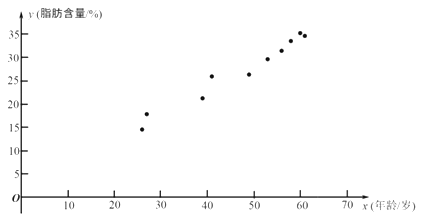
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数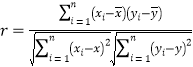
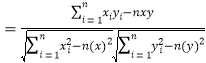
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为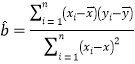 ,
,![]() .
.