题目内容
在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则 的值为
的值为
- A.-5
- B.-4
- C.4
- D.5
D
分析:由题意可得cos∠PDA= ,由
,由  =(
=( )•(
)•( ),再利用两个向量的数量积的定义,运算求得结果.
),再利用两个向量的数量积的定义,运算求得结果.
解答:由题意可得 ,
, ,|
,| |=|
|=| |=
|=
 =
= ,
,
∴tan∠PDA=2,cos∠PDA= .
.
∴ =(
=( )•(
)•( )=(
)=( )•(
)•( )
)
=- -
- +2
+2 =-5-2×
=-5-2× ×cos(π-∠PDA)+2×4
×cos(π-∠PDA)+2×4
=-5-2× ×(-
×(- )+8=5,
)+8=5,
故选D.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.
分析:由题意可得cos∠PDA=
 ,由
,由  =(
=( )•(
)•( ),再利用两个向量的数量积的定义,运算求得结果.
),再利用两个向量的数量积的定义,运算求得结果.解答:由题意可得
 ,
, ,|
,| |=|
|=| |=
|=
 =
= ,
,
∴tan∠PDA=2,cos∠PDA=
 .
.∴
 =(
=( )•(
)•( )=(
)=( )•(
)•( )
)=-
 -
- +2
+2 =-5-2×
=-5-2× ×cos(π-∠PDA)+2×4
×cos(π-∠PDA)+2×4=-5-2×
 ×(-
×(- )+8=5,
)+8=5,故选D.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
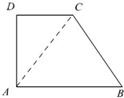
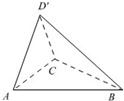
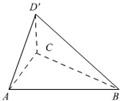
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
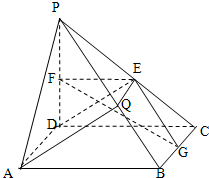
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为