题目内容
若不等式组
(其中
)表示的平面区域的面积是9．
（1）求
的值；（2）求
的最小值，及此时
与
的值．
（1）的值为
；（2）的最小值为
，此时
．
解析试题分析：（1）不等式组两两联立求出交点，由面积公式可直接求的值；（2）把看成点
与
两点的斜率，即可求出最小值及此时与的值．
（1）三个交点为
，因为,面积为
所以
6分
（2）
为点与两点的斜率，由图像知落在
时，最小，此时
，
． 12分
考点：线性规划问题、最值问题．
练习册系列答案
全程金卷系列答案
快乐5加2金卷系列答案
相关题目
、
，则集合
所表示的平面图形面积等于 
，其中
．
时，证明
；
在区间
，
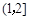内各有一个根，求
的取值范围；
的首项
，前
项和
，
，求
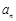，并判断
的二次函数
.
和
，分别从集合P和Q中随机取一个数作为
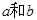，求函数
在区间
上是增函数的概率；
是区域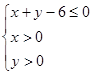
内的随机点，求函数
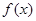在区间
的实数 
，不等式 
恒成立，则实数
的最大值是_______.
的最大值为 ；
的最小值 已知不等式
的解集与不等式
的解集相同，则
的值为（ ）
A． | B． |
C． | D． |