Question

若PA⊥平面ABC,AC⊥BC,PA=AC=1,BC=,求二面角APBC的余弦值.

Answer 1

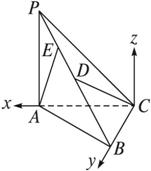
解法一:如图所示,取PB的中点D,连结CD.∵PC=BC=,

∴CD⊥PB.

∴作 AE⊥PB于E,那么二面角APBC的大小就等于异面直线DC与EA所成的角θ的大小.

∵PD=1,PE=,

∴DE=PD-PE=.

又∵AE=CD=1,AC=1,

∴cos(π-θ),

即1=+1-2··1·cosθ,

解得cosθ=.

故二面角APBC的余弦值为.

解法二:由解法一可知,向量的夹角的大小就是二面角APBC的大小,如上图,建立空间直角坐标系C—xyz,则A(1,0,0),B(0,,0),C(0,0,0),P(1,0,1),D为PB的中点,D().

∴,即E分的比为.

∴E(),

∴

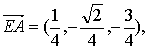
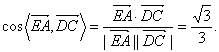
故二面角APBC的余弦值为.

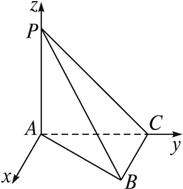
解法三:如图所示建立空间直角坐标系,则A(0,0,0),B(,1,0),C(0,1,0),P(0,0,1), =(0,0,1), =(,1,0),=(2,0,0),=(0,-1,1),

设平面PAB的法向量为m=(x,y,z),则

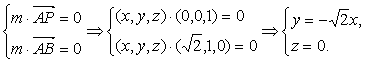
令x=1,则m=(1,-,0).

设平面PBC的法向量为n=(x′,y′,z′),则

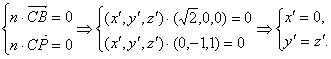
令y′=-1,则n=(0,-1,-1),

∴cos〈m,n〉=

∴二面角APBC的余弦值为.

绿色通道：

(1)求二面角的大小,可以在两个半平面内作出垂直于棱的两个向量,转化为这两向量的夹角,但应注意两向量的始点应在二面角的棱上.

(2)当空间直角坐标系容易建立(有特殊的位置关系)时,用向量法解较为简捷、明快.用法向量求二面角的大小时,有时不易判断两法向量的夹角的大小就是二面角的大小(相等或互补),但我们完全可以根据图形观察得到结论,这是因为二面角是钝二面角还是锐二面角一般是明显的.