题目内容
已知定义在(0,+∞)上的三个函数f(x)=lnx,g(x)=x2-af(x),h(x)=x-a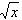 ,且g(x)在x=1处取得极值,
,且g(x)在x=1处取得极值,
(Ⅰ)求函数g(x)在x=2处的切线方程;
(Ⅱ)求函数h(x)的单调区间;
(Ⅲ)把h(x)对应的曲线C1向上平移6个单位后得到曲线C2,求C2与g(x)对应曲线C3的交点个数,并说明理由。
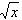 ,且g(x)在x=1处取得极值,
,且g(x)在x=1处取得极值,(Ⅰ)求函数g(x)在x=2处的切线方程;
(Ⅱ)求函数h(x)的单调区间;
(Ⅲ)把h(x)对应的曲线C1向上平移6个单位后得到曲线C2,求C2与g(x)对应曲线C3的交点个数,并说明理由。
解:(1)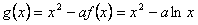 ,
,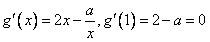 ,
,
∴a=2,经检验a=2成立,
又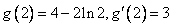 ,
,
∴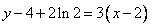 ,即3x-y-2-2ln2=0。
,即3x-y-2-2ln2=0。
(2)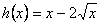 ,定义域[0,+∞),
,定义域[0,+∞),
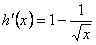 ,
,
令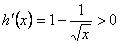 ,得x>1;令
,得x>1;令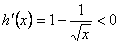 ,得0<x<1,
,得0<x<1,
∴函数h(x)单调递增区间是(1,+∞),单调递减区间是(0,1);
(3)由(1)知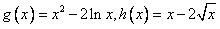 ,定义域[0,+∞),
,定义域[0,+∞),
∴C2对应的表达式为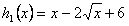 ,
,
问题转化为求函数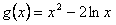 与
与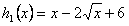 图象交点个数问题,
图象交点个数问题,
故只需求方程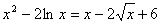 ,即
,即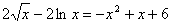 根的个数,
根的个数,
设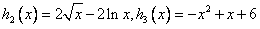 ,
,
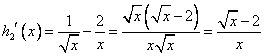 ,
,
当x∈(0,4),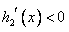 ,
,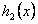 为减函数;当
为减函数;当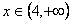 ,
,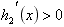 ,
,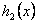 为增函数,
为增函数,
而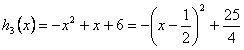 ,图象是开口向下的抛物线,
,图象是开口向下的抛物线,
作出函数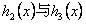 的图象,
的图象,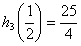 ,
,
而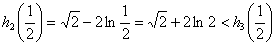 可知交点个数为2个,
可知交点个数为2个,
即曲线C2与C3的交点个数为2个。
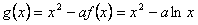 ,
,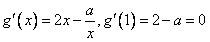 ,
, ∴a=2,经检验a=2成立,
又
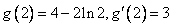 ,
,∴
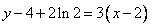 ,即3x-y-2-2ln2=0。
,即3x-y-2-2ln2=0。(2)
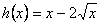 ,定义域[0,+∞),
,定义域[0,+∞), 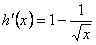 ,
,令
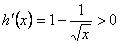 ,得x>1;令
,得x>1;令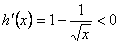 ,得0<x<1,
,得0<x<1,∴函数h(x)单调递增区间是(1,+∞),单调递减区间是(0,1);
(3)由(1)知
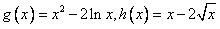 ,定义域[0,+∞),
,定义域[0,+∞), ∴C2对应的表达式为
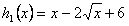 ,
,问题转化为求函数
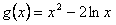 与
与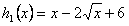 图象交点个数问题,
图象交点个数问题,故只需求方程
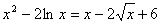 ,即
,即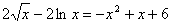 根的个数,
根的个数,设
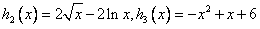 ,
,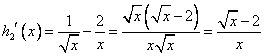 ,
,当x∈(0,4),
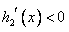 ,
,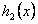 为减函数;当
为减函数;当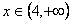 ,
,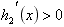 ,
,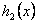 为增函数,
为增函数,而
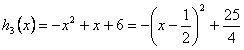 ,图象是开口向下的抛物线,
,图象是开口向下的抛物线,作出函数
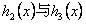 的图象,
的图象,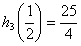 ,
,而
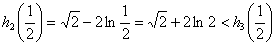 可知交点个数为2个,
可知交点个数为2个,即曲线C2与C3的交点个数为2个。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论: