题目内容
设函数
在[1，+∞）上是增函数．
（1）求正实数a的取值范围；
（2）设b＞0，a＞1，求证：
．
在[1，+∞）上是增函数．（1）求正实数a的取值范围；
（2）设b＞0，a＞1，求证：
．解：（1）
对x∈[1，+∞）恒成立，
∴
对x∈[1，+∞）恒成立，又
，
∴a≥1为所求；
（2）取
，∵
，
一方面，由（1）知
在[1，+∞）上是增函数，
∴
∴
即
；
另一方面，设函数G（x）=x﹣lnx（x＞1），
，
∴G（x）在（1，+∞）上是增函数且在x=x0处连续，
又G（1）=1＞0，
∴当x＞1时，G（x）＞G（1）＞0，
∴x＞lnx即
，
综上所述，
．
对x∈[1，+∞）恒成立，∴
对x∈[1，+∞）恒成立，又
，∴a≥1为所求；
（2）取
，∵
，一方面，由（1）知
在[1，+∞）上是增函数，∴
∴
即
；另一方面，设函数G（x）=x﹣lnx（x＞1），
，∴G（x）在（1，+∞）上是增函数且在x=x0处连续，
又G（1）=1＞0，
∴当x＞1时，G（x）＞G（1）＞0，
∴x＞lnx即
，综上所述，
．
练习册系列答案
相关题目
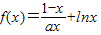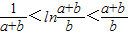在[1，+∞)上是增函数，
。
在[1，+∞）上是增函数．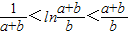
．
在[1，+∞）上是增函数．
．
在[1，+∞）上是增函数．
．