题目内容
已知函数,f(x)=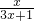 ,数列{an}满足a1=1,an+1=f(an)(n∈N*)
,数列{an}满足a1=1,an+1=f(an)(n∈N*)
(I)求证数列{ }是等差数列,并求数列{an}的通项公式;
}是等差数列,并求数列{an}的通项公式;
(II)记Sn=a1a2+a2a3+..anan+1,求Sn.
解:(I)由条件得,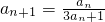 .
.
∴ ?
?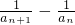 =3.
=3.
∴数列{ }是首项为
}是首项为 =1,公差d=3的等差数列.
=1,公差d=3的等差数列.
∴ =1+(n-1)×3=3n-2.
=1+(n-1)×3=3n-2.
故an= .
.
(II)∵anan+1= (
( ).
).
∴Sn═a1a2+a2a3+..anan+1
= [(1-
[(1- )+(
)+(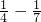 )+…+(
)+…+( )]
)]
= (1-
(1- )=
)=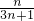 .
.
分析:(I)直接利用an+1=f(an)得到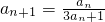 .再对其取倒数整理即可证数列{
.再对其取倒数整理即可证数列{ }是等差数列;进而求出数列{an}的通项公式;
}是等差数列;进而求出数列{an}的通项公式;
(II)利用(I)的结论以及所问问题的形式,直接利用裂项相消求和法即可求Sn.
点评:本题第二问主要考查了数列求和的裂项相消法.裂项相消法一般适用于一数列的通项是一分式形式且分子为常数,而分母是某一等差数列相邻两项的乘积组成.
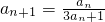 .
.∴
 ?
?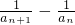 =3.
=3.∴数列{
 }是首项为
}是首项为 =1,公差d=3的等差数列.
=1,公差d=3的等差数列.∴
 =1+(n-1)×3=3n-2.
=1+(n-1)×3=3n-2.故an=
 .
.(II)∵anan+1=
 (
( ).
).∴Sn═a1a2+a2a3+..anan+1
=
 [(1-
[(1- )+(
)+(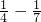 )+…+(
)+…+( )]
)]=
 (1-
(1- )=
)=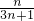 .
.分析:(I)直接利用an+1=f(an)得到
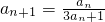 .再对其取倒数整理即可证数列{
.再对其取倒数整理即可证数列{ }是等差数列;进而求出数列{an}的通项公式;
}是等差数列;进而求出数列{an}的通项公式;(II)利用(I)的结论以及所问问题的形式,直接利用裂项相消求和法即可求Sn.
点评:本题第二问主要考查了数列求和的裂项相消法.裂项相消法一般适用于一数列的通项是一分式形式且分子为常数,而分母是某一等差数列相邻两项的乘积组成.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
