题目内容
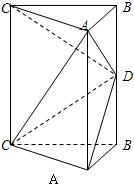
在四面体ABCD中，E，F分别是AC、BD的中点，若AB=2
，CD=4，EF⊥AB，则EF与CD所成之角______．
| 3 |
取BC的中点G，连接EG，FG，
由题意可得EG
AB，FG
CD，
∴∠EFG或其补角即为EF与CD所成的角，
∵EF⊥AB，∴EF⊥EG，
在RT△EFG中，sin∠EFG=
=
，
∴EF与CD所成的角为600
故答案为：60°
由题意可得EG
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
| 1 |
| 2 |
∴∠EFG或其补角即为EF与CD所成的角，
∵EF⊥AB，∴EF⊥EG，
在RT△EFG中，sin∠EFG=
| EG |
| FG |
| ||
| 2 |
∴EF与CD所成的角为600
故答案为：60°
练习册系列答案
相关题目
