Question

选修4-4：坐标系与参数方程

在平面直角坐标系xoy中，已知曲线C₁：x²+y²=1，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：ρ(2cosθ-sinθ)=6.

（Ⅰ）将曲线C₁上的所有点的横坐标，纵坐标分别伸长为原来的、2倍后得到曲线C₂，试写出直线l的直角坐标方程和曲线C₂的参数方程.

（Ⅱ）在曲线C₂上求一点P，使点P到直线l的距离最大，并求出此最大值．

Answer 1

解：（Ⅰ）由题意知，直线l的直角坐标方程为：2x-y-6=0.

∵C₂：（=1　∴C₂：的参数方程为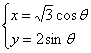：（θ为参数）……5分

（Ⅱ）设P（cosθ，2sinθ），则点P到l的距离为：

d=，

∴当sin(60°-θ)＝-1即点P（-,1）时，此时d_wax=[=2……10分