题目内容
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4。
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为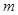 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求

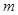 +2的概率。
+2的概率。
(1) (2)
(2)
解析试题分析:(1)从袋中随机抽取两个球,是随机事件,基本事件数为6,其中编号之和不大于4的有2情况
根据随机事件的概率公式可求得取出的球的编号之和不大于4的概率为 ;(2)抽取的结果是(m,n),写出所有的可能结果总数,,找出取值
;(2)抽取的结果是(m,n),写出所有的可能结果总数,,找出取值

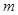 +2的结果数,由随机事件的概率公式可求出
+2的结果数,由随机事件的概率公式可求出

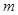 +2的概率
+2的概率
试题解析:(1)从袋中随机抽取两个球,其一切可能结果组成的基本事件由(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6个,从袋中随机抽取两个球,取出的球的编号之和不大于4的事件有1,2),(1,3)2个,
因此所求事件的 概率为 .
.
(2))先从袋中随机取一个球,记下球的编号为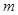 ,放回后,再从袋中随机取一个球,记下球的编号为
,放回后,再从袋中随机取一个球,记下球的编号为 ,其一切可能结果(m,n)有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,满足条件
,其一切可能结果(m,n)有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个,满足条件

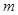 +2有13个,根据随机事件的概率公式可得,
+2有13个,根据随机事件的概率公式可得,

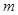 +2的概率为
+2的概率为 .
.
考点:随机事件的概率.

练习册系列答案
相关题目
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 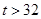 ℃ ℃ |
| 天数 | 6 | 12 | 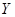 | 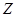 |
某水果商根据多年的销售经验,六月份的日最高气温t (单位:℃)对西瓜的销售影响如下表:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃<t 28℃ 28℃ | 28℃<t 32℃ 32℃ | 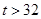 ℃ ℃ |
日销售额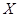 (千元) (千元) | 2 | 5 | 6 | 8 |
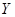 ,
, 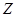 的值;
的值;(Ⅱ) 若视频率为概率,求六月份西瓜日销售额的期望和方差;
(Ⅲ) 在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
 ,道路C,E上下班时间往返出现拥堵的概率都是
,道路C,E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.
 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。 道备选试验考查题中一次随机抽取
道备选试验考查题中一次随机抽取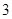 题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中
题,并按照题目要求独立完成全部实验操作.规定:至少正确完成其中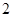 题便通过考查.已知
题便通过考查.已知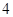 题能正确完成,
题能正确完成,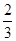 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.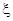 和文科考生乙正确完成题数
和文科考生乙正确完成题数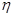 的概率分布列,并计算各自的数学期望;
的概率分布列,并计算各自的数学期望;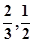 且每棵树是否存活互不影响,求移栽的5棵树中:
且每棵树是否存活互不影响,求移栽的5棵树中: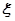 的分布列与期望.
的分布列与期望.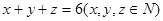 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;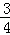 、
、 、
、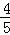 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.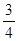 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为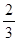 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.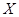 的分布列及数学期望
的分布列及数学期望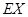 ;
;