题目内容
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.(1)证明:BD⊥平面PAC;
(2)若AD=2,当PC与平面ABCD所成角的正切值为
| ||
| 2 |
分析:(1)由PA⊥平面ABCD,PC⊥平面BDE,结合线面垂直的性质可得PA⊥BD及PC⊥BD,进而由线面垂直的判定定理可得BD⊥平面PAC;
(2)由已知可得PC即为四棱锥P-ABCD的外接球的直径,结合AD=2,PC与平面ABCD所成角的正切值为
时,求出外接球的半径,可得四棱锥P-ABCD的外接球表面积.
(2)由已知可得PC即为四棱锥P-ABCD的外接球的直径,结合AD=2,PC与平面ABCD所成角的正切值为
| ||
| 2 |
解答: 证明:(1)∵PA⊥平面ABCD,BD?平面ABCD,
证明:(1)∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD.…(2分)
同理由PC⊥平面BDE可证得PC⊥BD. …(4分)
又PA∩PC=P,
∴BD⊥平面PAC. …(6分)
解:(2)由(1)知BD⊥平面PAC,又AC?平面PAC,
∴BD⊥AC.
故矩形ABCD为正方形,
∴AB=BC=CD=AD=2.
所以AC=2
…(8分)
因为PA⊥平面ABCD,
所以 PA与平面ABCD所成角为∠PCA,
因为PC与平面ABCD所成角的正切值为
,
即tan∠PCA=
,即tan∠PCA=
,
所以PA=ACtan∠PAC=2
×
=2,…(10分)
又2R=PC=
=
,
∴R=
所以四棱锥P-ABCD的外接球体积为S球面=4πR2=4π(
)2=12π.…(12分)
 证明:(1)∵PA⊥平面ABCD,BD?平面ABCD,
证明:(1)∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD.…(2分)
同理由PC⊥平面BDE可证得PC⊥BD. …(4分)
又PA∩PC=P,
∴BD⊥平面PAC. …(6分)
解:(2)由(1)知BD⊥平面PAC,又AC?平面PAC,
∴BD⊥AC.
故矩形ABCD为正方形,
∴AB=BC=CD=AD=2.
所以AC=2
| 2 |
因为PA⊥平面ABCD,
所以 PA与平面ABCD所成角为∠PCA,
因为PC与平面ABCD所成角的正切值为
| ||
| 2 |
即tan∠PCA=
| ||
| 2 |
| PA |
| AC |
所以PA=ACtan∠PAC=2
| 2 |
| ||
| 2 |
又2R=PC=
| 22+22+22 |
| 12 |
∴R=
| 3 |
所以四棱锥P-ABCD的外接球体积为S球面=4πR2=4π(
| 3 |
点评:本题考查的知识点是直线与平面垂直的判定,球的表面积,解答(1)的关键是熟练掌握线面垂直的判定与性质,解答(2)的关键是求出四棱锥P-ABCD的外接球的半径.

练习册系列答案
相关题目
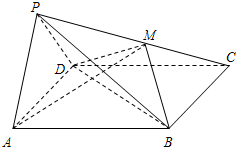 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.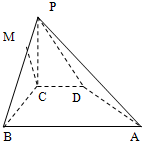 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB