题目内容
设函数![]() ,
,
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若关于x的方程![]() 内恰有两个相异的实根,求实数a的取值范围。
内恰有两个相异的实根,求实数a的取值范围。
解:(1)函数![]() 的定义域
的定义域![]() ,
,
![]()
![]() 的取值范围为
的取值范围为![]()
![]()
(2)方法1:![]()
![]()
令![]()
![]()
由![]()
![]() 在区间[1,2]内单调递减,在区间[2,3]内单调递增,
在区间[1,2]内单调递减,在区间[2,3]内单调递增,
故![]() 内恰有两个相异实根
内恰有两个相异实根
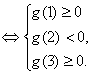
即
综上所述,a的取值范围是[2ln3-4,2ln2-3![]() 。
。
方法2:![]()
![]()
即![]()
令![]()
![]()
由![]()
![]() 在区间[1,2]内单调递增,在区间[2,3]内单调递减。
在区间[1,2]内单调递增,在区间[2,3]内单调递减。
![]()
![]()
故![]() 内恰有两个相异实根
内恰有两个相异实根
![]()
![]()
综上所述,a的取值范围是[2ln3-4,2ln2-3![]() 。
。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
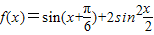 .
. ,求b值.
,求b值. .
. ,求a的值.
,求a的值.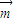 =(
=(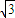 sin2x-1,cosx),
sin2x-1,cosx),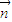 =(1,2cosx),设函数
=(1,2cosx),设函数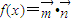 .
.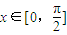 时的最大值;
时的最大值; .
. 的单调区间;
的单调区间; .
.