题目内容
6.已知函数f(x)=ax3+3xlnx-1(a∈R).(Ⅰ)当a=0时,求f(x)的极值;
(Ⅱ)若f(x)在区间$(\frac{1}{e},e)$(其中e=2.71 828…)上有且只有一个极值点,求实数a的取值范围.
分析 (1)当a=0时,化简函数f(x)=3xlnx-1并求定义域,再求导数f′(x)=3lnx+3=3(lnx+1),从而由导数确定函数的极值;
(2)函数f(x)=ax3+3xlnx-1的定义域为(0,+∞),再求导f′(x)=3(ax2+lnx+1),再令g(x)=ax2+lnx+1,再求导g′(x)=2ax+=,从而由导数的正负性分类讨论以确定函数是否有极值点及极值点的个数.
解答 解:(Ⅰ)当a=0时,f(x)=3xlnx-1,
∴f′(x)=3(lnx+1),
令f′(x)=0,解得x=$\frac{1}{e}$,
当x∈(0,$\frac{1}{e}$)时,f′(x)<0,函数单调递减,
当x∈($\frac{1}{e}$,+∞)时,f′(x)>0,函数单调递增,
∴当x=$\frac{1}{e}$时,函数f(x)有极小值f($\frac{1}{e}$)=-$\frac{3}{e}$-1,
(Ⅱ)函数f(x)=ax3+3xlnx-1的定义域为(0,+∞),
f′(x)=3(ax2+lnx+1),
令g(x)=ax2+lnx+1,则g′(x)=2ax+$\frac{1}{x}$=$\frac{2a{x}^{2}+1}{x}$,
当a>0时,g′(x)>0在(0,+∞)恒成立,
故f′(x)=3(ax2+lnx+1)在(0,+∞)上是增函数,
而f′($\frac{1}{e}$)=3[a($\frac{1}{e}$)2+ln+1]=3a($\frac{1}{e}$)2>0,
故当x∈($\frac{1}{e}$,e)时,f′(x)>0恒成立,
故f(x)在区间($\frac{1}{e}$,e)上单调递增,
故f(x)在区间($\frac{1}{e}$,e)上没有极值点;
当a=0时,由(1)知,f(x)在区间($\frac{1}{e}$,e)上没有极值点;
当a<0时,令=$\frac{2a{x}^{2}+1}{x}$=0解得,x=$\sqrt{-\frac{1}{2a}}$;
故g(x)=ax2+lnx+1在(0,$\sqrt{-\frac{1}{2a}}$)上是增函数,在($\sqrt{-\frac{1}{2a}}$,+∞)上是减函数,
①当g(e)•g($\frac{1}{e}$)<0,即-$\frac{2}{{e}^{2}}$<a<0时,
g(x)在($\frac{1}{e}$,e)上有且只有一个零点,且在该零点两侧异号,
②令g($\frac{1}{e}$)=0得=0,不可能;
③令g(e)=0得a=-$\frac{2}{{e}^{2}}$,所以∈($\sqrt{-\frac{1}{2a}}$,e),
而g($\sqrt{-\frac{1}{2a}}$)=g($\frac{e}{2}$)=$\frac{1}{2}$+ln$\frac{e}{2}$>0,
又g($\frac{1}{e}$)<0,
所以g(x)在($\frac{1}{e}$,e)上有且只有一个零点,且在该零点两侧异号,
综上所述,实数a的取值范围是[-$\frac{2}{{e}^{2}}$,0).
点评 本题考查了导数的综合应用及分类讨论的思想应用,化简比较困难,属于难题.

| A. | 1 | B. | -1 | C. | -$\frac{3}{4}$ | D. | -2 |
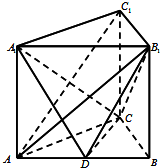 如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.
如图,三棱柱ABC-A1B1C1侧棱垂直于底面,AB=4,AC=BC=3,D为AB的中点.