题目内容
若平面向量 ,
, ,
, 两两所成的角相等,|
两两所成的角相等,| |=|
|=| |=1,|
|=1,| |=3,则|
|=3,则| +
+ +
+ |=________.
|=________.
2或5
分析:设向量所成的角为α,则α=0°或α=120°,先求出 的值即可求出.
的值即可求出.
解答:由向量 、
、 、
、 两两所成的角相等,设向量所成的角为α,由题意可知α=0°或α=120°,
两两所成的角相等,设向量所成的角为α,由题意可知α=0°或α=120°,
则 =
= +
+ +
+ +2(
+2( +
+ +
+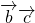 )=11+2(|
)=11+2(| |•|
|•| |cosα+|
|cosα+| |•|
|•| |cosα+|
|cosα+| |•|
|•| |cosα)=11+14cosα.
|cosα)=11+14cosα.
所以当α=0°时,| +
+ +
+ |=5;
|=5;
当α=120°时,| +
+ +
+ |=2.
|=2.
故答案为 2或5.
点评:考查学生会计算平面向量的数量积,灵活运用 =|
=| |•|
|•| |cosα的公式,求向量的模的方法,属于基础题.
|cosα的公式,求向量的模的方法,属于基础题.
分析:设向量所成的角为α,则α=0°或α=120°,先求出
 的值即可求出.
的值即可求出.解答:由向量
 、
、 、
、 两两所成的角相等,设向量所成的角为α,由题意可知α=0°或α=120°,
两两所成的角相等,设向量所成的角为α,由题意可知α=0°或α=120°,则
 =
= +
+ +
+ +2(
+2( +
+ +
+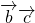 )=11+2(|
)=11+2(| |•|
|•| |cosα+|
|cosα+| |•|
|•| |cosα+|
|cosα+| |•|
|•| |cosα)=11+14cosα.
|cosα)=11+14cosα.所以当α=0°时,|
 +
+ +
+ |=5;
|=5;当α=120°时,|
 +
+ +
+ |=2.
|=2.故答案为 2或5.
点评:考查学生会计算平面向量的数量积,灵活运用
 =|
=| |•|
|•| |cosα的公式,求向量的模的方法,属于基础题.
|cosα的公式,求向量的模的方法,属于基础题. 
练习册系列答案
相关题目
 、
、 、
、 两两所成的角相等,且
两两所成的角相等,且 ,
,
 ,
, ,
, 两两所成的角相等,|
两两所成的角相等,| |=|
|=| |=1,|
|=1,| |=3,则|
|=3,则| +
+ +
+ |= .
|= . ,
, ,
, 两两所成的角相等,|
两两所成的角相等,| |=|
|=| |=1,|
|=1,| |=3,则|
|=3,则| +
+ +
+ |=( )
|=( )