题目内容

三角形的面积为S=(a+b+c)r,a、b、c为三角形的边长，r为三角形内切圆的半径，利用类比推理，求出四面体的体积公式.

解:V=(S1+S2+S3+S4)r(S1、S2、S3、S4分别为四个面的面积,r为内切球半径),

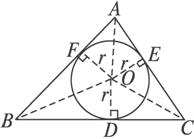
设△ABC的三边与⊙O分别切于D、E、F,

则OD⊥BC,OE⊥AC,OF⊥AB且OD=OE=OF=r.

连结OA、OB、OC,

则S△ABC=S△OAB+S△OAC+S△OBC=cr+br+ar=(a+b+c)r.

类似地,三棱锥P—ABC的内切球为球O,半径为r,则球心O到各面的距离都为r,

四个面的面积分别为S1、S2、S3、S4,

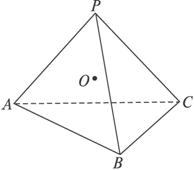
则VP—ABC=VO—ABC+VO—PBC+VO—PAC+VO—PAB

=S1r+S2r+S3r+S4r

=(S1+S2+S3+S4)r.

练习册系列答案
相关题目
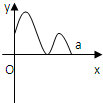
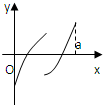
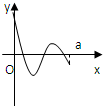
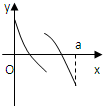
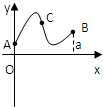精英家教网定义在区间[0，a]上的函数f（x）的图象如图所示，记以A（0，f（0）），B（a，f（a）），C（x，f（x））为顶点的三角形的面积为S（x），则函数S（x）的导函数S′（x）的图象大致是（　　）
A、精英家教网B、精英家教网C、精英家教网D、精英家教网
三角形的面积为S=
1
2
(a+b+c)•r，其中a，b，c为三角形的边长，r为三角形内切圆的半径，设S1、S2、S3、S4分别为四面体四个面的面积，r为四面体内切球的半径，利用类比推理可以得到四面体的体积为
V=
1
3
(S1+S2+S3+S4)r
V=
1
3
(S1+S2+S3+S4)r
．
已知三角形的三边分别为a，b，c，内切圆的半径为r，则三角形的面积为s=
1
2
（a+b+c）r；四面体的四个面的面积分别为s1，s2，s3，s4，内切球的半径为R．类比三角形的面积可得四面体的体积为（　　）
三角形的面积为S=
1
2
(a+b+c)r，a、b、c为三角形的边长，r为三角形内切圆的半径，利用类比推理可以得出四面体的体积为
V=
1
3
（S1+S2+S3+S4）r
V=
1
3
（S1+S2+S3+S4）r
．
设A，B，C为△ABC的三内角，其对边分别为a，b，c，若
m
=(-cos
A
2
，sin
A
2
)，
n
=(cos
A
2
，sin
A
2
)且
m
•
n
=
1
2

（Ⅰ）求角A的大小；
（Ⅱ）若a=2
3
，三角形的面积为S=
3
，求△ABC的周长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网