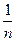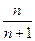题目内容
(本小题满分10分)
设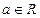 ,函数
,函数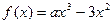 .
.
(Ⅰ) 若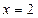 是函数
是函数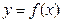 的极值点,求实数
的极值点,求实数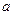 的值;
的值;
(Ⅱ)求函数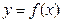 在区间
在区间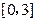 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)若函数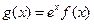 在
在 上是单调递减函数,求实数
上是单调递减函数,求实数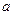 的取值范围.
的取值范围.
设
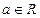 ,函数
,函数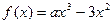 .
.(Ⅰ) 若
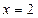 是函数
是函数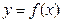 的极值点,求实数
的极值点,求实数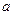 的值;
的值;(Ⅱ)求函数
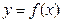 在区间
在区间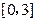 上的最大值和最小值;
上的最大值和最小值;(Ⅲ)若函数
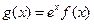 在
在 上是单调递减函数,求实数
上是单调递减函数,求实数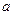 的取值范围.
的取值范围.解:(Ⅰ) 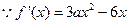 ,
,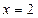 是函数
是函数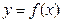 的极值点
的极值点
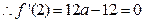
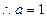
(Ⅱ)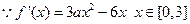 下面分类讨论:
下面分类讨论:
①当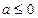 时,因为
时,因为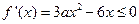 ,易知
,易知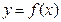 在
在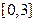 上是减函数,
上是减函数,
所以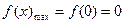 ,
,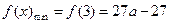 ;
;
②当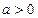 时,因为
时,因为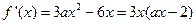 ,
,
令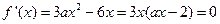 得
得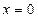 或
或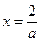 ;
;
令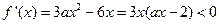 得
得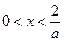 ;
;
令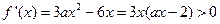 得
得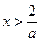 或
或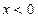 ;
;
若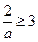 ,即
,即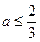 时,
时, 在
在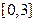 上是减函数,
上是减函数,
所以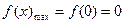 ,
,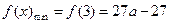 ;
;
若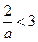 ,即
,即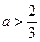 时,易知
时,易知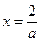 是
是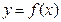 在
在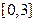 内的极小值点也是最小值点,
内的极小值点也是最小值点,
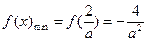 ,
,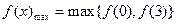
当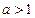 时,
时,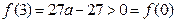 ,
,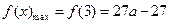 ;
;
当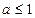 时,
时,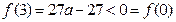 ,
,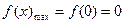 ;
;
综上所述,当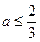 时,
时,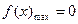 ,
,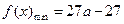 ;
;
当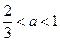 时,
时,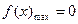 ,
,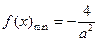 ;
;
当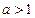 时,
时,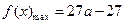 ,
,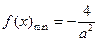 .
.
(Ⅲ) 因为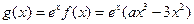 在
在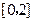 上是单调递减函数,
上是单调递减函数,
所以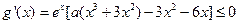 ,
, 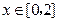
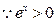
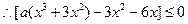
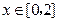
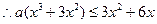
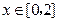
当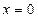 时,
时,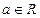 ,都有
,都有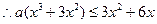 成立;
成立;
当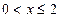 时,
时,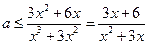 .
.
记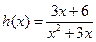 ,
,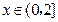
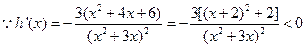
 在
在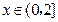 上单调递减,
上单调递减,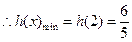
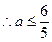
综上所述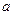 的取值范围是
的取值范围是 .
.
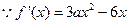 ,
,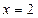 是函数
是函数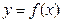 的极值点
的极值点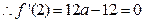
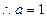
(Ⅱ)
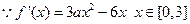 下面分类讨论:
下面分类讨论:①当
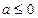 时,因为
时,因为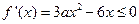 ,易知
,易知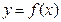 在
在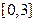 上是减函数,
上是减函数,所以
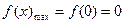 ,
,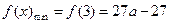 ;
;②当
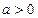 时,因为
时,因为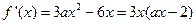 ,
,令
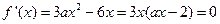 得
得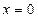 或
或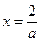 ;
;令
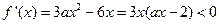 得
得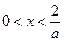 ;
;令
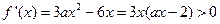 得
得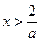 或
或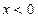 ;
;若
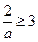 ,即
,即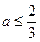 时,
时,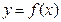 在
在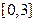 上是减函数,
上是减函数,所以
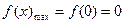 ,
,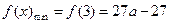 ;
;若
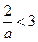 ,即
,即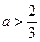 时,易知
时,易知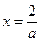 是
是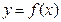 在
在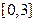 内的极小值点也是最小值点,
内的极小值点也是最小值点,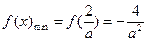 ,
,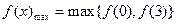
当
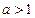 时,
时,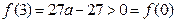 ,
,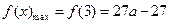 ;
;当
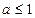 时,
时,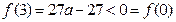 ,
,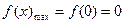 ;
;综上所述,当
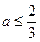 时,
时,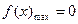 ,
,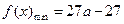 ;
;当
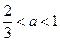 时,
时,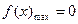 ,
,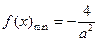 ;
;当
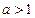 时,
时,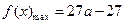 ,
,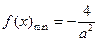 .
.(Ⅲ) 因为
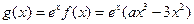 在
在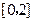 上是单调递减函数,
上是单调递减函数, 所以
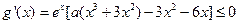 ,
, 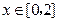
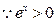
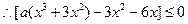
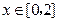
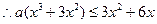
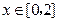
当
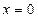 时,
时,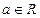 ,都有
,都有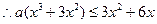 成立;
成立;当
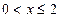 时,
时,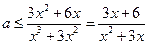 .
.记
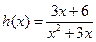 ,
,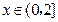
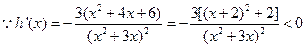
 在
在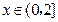 上单调递减,
上单调递减,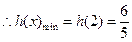
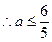
综上所述
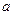 的取值范围是
的取值范围是 .
.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
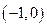 作抛物线
作抛物线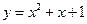 的切线方程.
的切线方程. 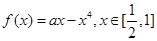 ,A、B是图像上不同的两点,若直线AB的斜率k总满足
,A、B是图像上不同的两点,若直线AB的斜率k总满足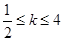 ,则实数a的值是 ( )
,则实数a的值是 ( )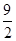 B.
B.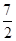 C.5 D.1
C.5 D.1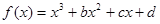 图象如图,则函数
图象如图,则函数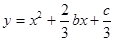 的单调递增区间为( )
的单调递增区间为( )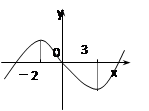

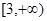

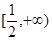
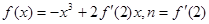 ,则二项式
,则二项式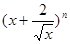 展开式中常数
展开式中常数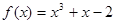 在
在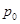 处的切线平行于直线
处的切线平行于直线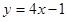 ,则
,则
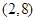

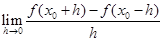 =( )
=( )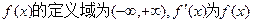 的导函数,函数
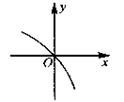
的导函数,函数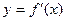 的图象如图所示,且
的图象如图所示,且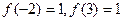 ,则不等式
,则不等式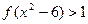 的
的 解集为( **
解集为( ** *)
*)
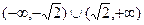
 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为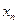 ,则
,则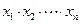 的值为( )
的值为( )