题目内容
8.在四面体ABCD中,下列条件不能得出AB⊥CD的是( )| A. | AB⊥BC且AB⊥BD | B. | AD⊥BC且AC⊥BD | C. | AC=AD且BC=BD | D. | AC⊥BC且AD⊥BD |
分析 在几何体中选取边长的中点,运用等腰三角形的性质,直线平面的垂直,平面与平面的垂直问题判断即可得出答案.
解答 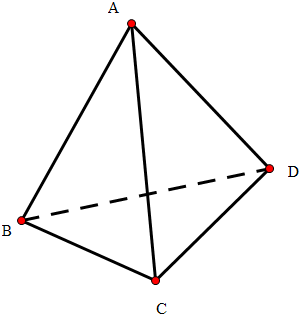 解:①∵AB⊥BD,AB⊥BC,BD∩BC=B,
解:①∵AB⊥BD,AB⊥BC,BD∩BC=B,
∴AB⊥面BCD,
∵CD?面BCD,
∴AB⊥CD,
②设A在面BCD射影为O,AO⊥面BCD,
∵AD⊥BC,AC⊥BD,
∴O为△BCD的垂心
连接BO,则BO⊥CD,AO⊥CD
∴CD⊥面ABO.
∵AB?面ABO.
∴AB⊥CD,
③取CD中点G,连接BG,AG,
∵AC=AD且BC=BD,
∴CD⊥BG,CD⊥AG,
∵BG∩AG=G,
∴CD⊥面ABG,
∵AB?面ABG
∴AB⊥CD,
综上选项A,B,C能够得出AB⊥CD,
故选:D
点评 本题综合考查了空间几何体中点直线,平面的垂直问题,关键是利用平面几何知识,空间直线平面的性质定理,判定定理转化直线的位置关系判断即可.

练习册系列答案
相关题目
3.在静水中划船的速度是每分钟40m,水流的速度是每分钟20m,如果船从岸边A处出发,沿着与水流垂直的航线到达对岸,那么船前进的方向指向河流的上游并与河岸垂直的方向所成的角为( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
20.二面角α-l-β为θ,a⊥α,b⊥β,且a与b为异面直线,则a与b所成角( )
| A. | θ | B. | π-θ | C. | $\frac{π}{2}$+θ | D. | θ或π-θ |