Question

【题目】在平面直角坐标系中，动点分别与两个定点，的连线的斜率之积为.

（1）求动点的轨迹的方程；

（2）设过点的直线与轨迹交于，两点，判断直线与以线段为直径的圆的位置关系，并说明理由.

Answer 1

【答案】（1） ； （2）相离.

【解析】

（1）根据直接法求轨迹方程，（2）先用坐标表示以线段为直径的圆方程，再根据圆心到直线距离与半径大小进行判断.

（1）设动点的坐标为，

因为 ， ，

所以，整理得．

所以动点的轨迹的方程 ．

（2）过点的直线为轴时，显然不合题意．

所以可设过点的直线方程为，

设直线与轨迹的交点坐标为 ，，

由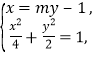得．

因为，

由韦达定理得 =， =．

注意到 =．

所以的中点坐标为．

因为 ．

点到直线的距离为．

因为 ，即 ，

所以直线与以线段为直径的圆相离．