题目内容
已知数列an满足
(1)求数列an的通项公式an;
(2)设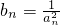 ,求数列bn的前n项和Sn;
,求数列bn的前n项和Sn;
(3)设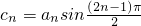 ,,数列cn的前n项和为Tn.
,,数列cn的前n项和为Tn.
求证:对任意的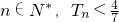
解:(1)∵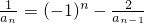 ,∴
,∴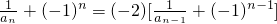 ,
,
又∵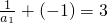 ,所以数列
,所以数列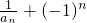 (n∈N*)是以3为首项,-2为公比的等比数列,
(n∈N*)是以3为首项,-2为公比的等比数列,
∴ .
.
(2)bn=(3×2n-1+1)2
=9•4n-1+6•2n-1+1,
∴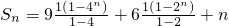
=3•4n+6•2n+n-9.
(3)证明:由(1)知 ,当n≥3时,则
,当n≥3时,则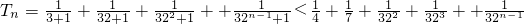
=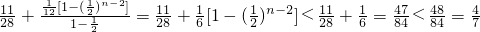
又∵T1<T2<T3,
∴对任意的n∈N*,Tn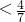 .(12分)
.(12分)
分析:(1)由题意知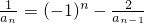 ,所以
,所以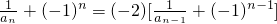 ,再由
,再由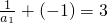 ,知数列
,知数列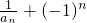 (n∈N*)是以3为首项,-2为公比的等比数列,由此可求出数列an的通项公式an.
(n∈N*)是以3为首项,-2为公比的等比数列,由此可求出数列an的通项公式an.
(2)由题设知bn=(3×2n-1+1)2=9•4n-1+6•2n-1+1,所以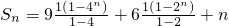
=3•4n+6•2n+n-9.
(3)由题意知 ,
,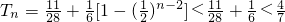 ,再由T1<T2<T3,知对任意的n∈N*,Tn
,再由T1<T2<T3,知对任意的n∈N*,Tn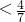 .
.
点评:本题考查数列的应用和性质,解题时要认真审题,注意公式的灵活运用,注意积累解题方法.
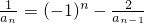 ,∴
,∴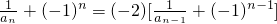 ,
,又∵
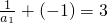 ,所以数列
,所以数列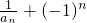 (n∈N*)是以3为首项,-2为公比的等比数列,
(n∈N*)是以3为首项,-2为公比的等比数列,∴
 .
.(2)bn=(3×2n-1+1)2
=9•4n-1+6•2n-1+1,
∴
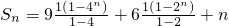
=3•4n+6•2n+n-9.
(3)证明:由(1)知
 ,当n≥3时,则
,当n≥3时,则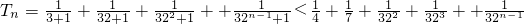
=
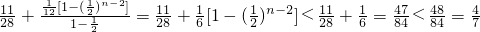
又∵T1<T2<T3,
∴对任意的n∈N*,Tn
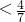 .(12分)
.(12分)分析:(1)由题意知
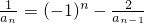 ,所以
,所以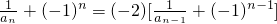 ,再由
,再由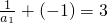 ,知数列
,知数列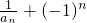 (n∈N*)是以3为首项,-2为公比的等比数列,由此可求出数列an的通项公式an.
(n∈N*)是以3为首项,-2为公比的等比数列,由此可求出数列an的通项公式an.(2)由题设知bn=(3×2n-1+1)2=9•4n-1+6•2n-1+1,所以
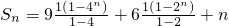
=3•4n+6•2n+n-9.
(3)由题意知
 ,
,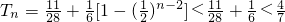 ,再由T1<T2<T3,知对任意的n∈N*,Tn
,再由T1<T2<T3,知对任意的n∈N*,Tn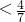 .
.点评:本题考查数列的应用和性质,解题时要认真审题,注意公式的灵活运用,注意积累解题方法.

练习册系列答案
相关题目

 ,求数列bn的前n项和Sn;
,求数列bn的前n项和Sn;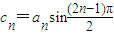 ,数列cn的前n项和为Tn.求证:对任意的
,数列cn的前n项和为Tn.求证:对任意的 .
.