题目内容

曲线
x2
25
-
y2
9
=1与曲线
x2
25-k
-
y2
9+k
=1(-9＜k＜25)的（　　）
A．实轴长相等B．虚轴长相等C．离心率相等D．焦距相等
∵-9＜k＜25，∴25-k＞0且9+k＞0
可得曲线
x2
25-k
-
y2
9+k
=1(-9＜k＜25)是焦点位于x轴的双曲线
∴c=
(25-k)+(9+k)
=4，得焦点坐标为（±
34
，0）
又∵曲线
x2
25
-
y2
9
=1也表示焦点在x轴的双曲线，易得它的焦点坐标为（±
34
，0）
∴两个曲线有相同的焦点坐标，故焦距相等
故选：D
练习册系列答案
相关题目
若双曲线的焦点为F1（-4，0），F2（4，0），实轴长与虚轴长相等，则双曲线的标准方程为：______．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线方程为y=±2x，则其离心率为（　　）
A．5B．
5
2
C．
3
D．
5
如图，F1，F2是双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，过F1的直线l与C的左、右分支分别交于A，B两点．若AB：BF2：AF2=3：4：5，则双曲线的离心率为______．
双曲线
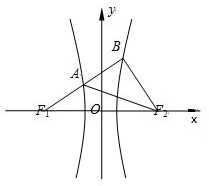
x2
a2
-
y2
b2
=1（a＞1，b＞0）的焦点距为2c，直线l过点（a，0）和（0，b），且点（1，0）到直线l的距离与点（-1，0）到直线l的距离之和s≥
4
5
c．求双曲线的离心率e的取值范围．
双曲线的方程为
x2
16
-
y2
9
=1，则其离心率为（　　）
A．
4
5
B．
5
4
C．±
4
5
D．±
5
4
若双曲线
x2
16
-
y2
m
=1的焦距为10，则双曲线的渐近线方程为______．
当m∈[-2，-1]时，二次曲线
x2
4
+
y2
m
=1的离心率e的取值范围是（　　）
A．[
2
2
，
3
2
]		B．[
3
2
，
5
2
]		C．[
5
2
，
6
2
]		D．[
3
2
，
6
2
]
双曲线C：x2-y2=2右支上的弦AB过右焦点F．
（1）求弦AB的中点M的轨迹方程
（2）是否存在以AB为直径的圆过原点O？若存在，求出直线AB的斜率K的值．若不存在，则说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网