题目内容
【题目】以直角坐标系xOy的原点为极坐标系的极点,x轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,P是
,P是![]() 上一动点,
上一动点,![]() ,Q的轨迹为
,Q的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程,
的极坐标方程,并化为直角坐标方程,
(2)若点![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与曲线
(t为参数),直线l与曲线![]() 的交点为A,B,当
的交点为A,B,当![]() 取最小值时,求直线l的普通方程.
取最小值时,求直线l的普通方程.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)设点P,Q的极坐标分别为![]() ,
,![]() ),利用
),利用![]() 这一关系,可得Q的极坐标方程,再化成普通方程,即可得答案;
这一关系,可得Q的极坐标方程,再化成普通方程,即可得答案;
(2)设点A,B对应的参数分别为![]() ,
,![]() ,则
,则![]() ,将直线l的参数方程
,将直线l的参数方程![]() ,(
,(![]() 为参数),代入
为参数),代入![]() 的直角坐标方程,利用韦达定理,从而将问题转化为三角函数的最值问题,求出此时的
的直角坐标方程,利用韦达定理,从而将问题转化为三角函数的最值问题,求出此时的![]() 值,即可得答案.
值,即可得答案.
(1)设点P,Q的极坐标分别为![]() ,
,![]() ),
),
因为![]() ,
,
所以曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
两边同乘以ρ,得![]() ,
,
所以![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() .
.
(2)设点A,B对应的参数分别为![]() ,
,![]() ,则
,则![]() ,
,
将直线l的参数方程![]() ,(
,(![]() 为参数),
为参数),
代入![]() 的直角坐标方程
的直角坐标方程![]() 中,整理得
中,整理得![]() .由根与系数的关系得
.由根与系数的关系得![]() .
.
∴![]()
![]()
![]() ,( 当且仅当
,( 当且仅当![]() 时,等号成立)
时,等号成立)
∴当![]() 取得最小值时,直线l的普通方程为
取得最小值时,直线l的普通方程为![]() .
.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
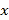
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式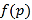 .
.


