Question

【题目】椭圆经过点,且离心率为.

（Ⅰ）求椭圆的方程；

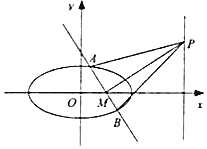
（Ⅱ）过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点，使得？若存在，求出点的坐标；若不存在，请说明理由。

Answer 1

【答案】（I）（II）存在点，使得.

【解析】试题分析：（1）由椭圆的标准方程和几何性质，即可求解的值，得到椭圆的标准方程；

（2）若存在点，由题意，当直线和的斜率存在,分别设为,，

等价于，直线的斜率存在，故设直线的方程为.

由 ，得，得，由，即可求得的值。

试题解析：（I）

（II）若存在点，使得，

则直线和的斜率存在,分别设为,.

等价于.

依题意，直线的斜率存在，故设直线的方程为.

由，得.

因为直线与椭圆有两个交点，所以.

即，解得.

设， ,则， ，

令，

当时， ，

化简得， ，

所以.

当时，也成立.

所以存在点，使得.