题目内容
若不等式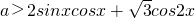
恒成立，则实数a的取值范围为________．
（2，+∞）
分析：令f（x）=2sinxcosx+
cos2x，则f（x）=2sin（2x+
），由题意可得，于是问题得到解决．
解答：令f（x）=2sinxcosx+cos2x=2sin（2x+），
∴不等式a＞2sinxcosx+cos2x恒成立，
就是a＞f（x）max成立，而f（x）max=2，
∴a＞2．
∴实数a的取值范围为（2，+∞）．
点评：本题考查三角函数的化简求值，理解题意得到a＞f（x）max是关键，属于基础题．
分析：令f（x）=2sinxcosx+
cos2x，则f（x）=2sin（2x+），由题意可得，于是问题得到解决．解答：令f（x）=2sinxcosx+
cos2x=2sin（2x+），∴不等式a＞2sinxcosx+
cos2x恒成立，就是a＞f（x）max成立，而f（x）max=2，
∴a＞2．
∴实数a的取值范围为（2，+∞）．
点评：本题考查三角函数的化简求值，理解题意得到a＞f（x）max是关键，属于基础题．
练习册系列答案
小学课时特训系列答案
相关题目
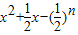≥0对任意n∈N*在x∈（-∞，λ]恒成立，则实常数λ的取值范围是 ．
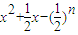≥0对任意n∈N*在x∈（-∞，λ]恒成立，则实常数λ的取值范围是 ．
,若对任意
及
该不等式恒成立，则实
的取值范围是 ▲ 。