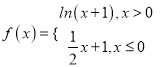题目内容
【题目】定义在（0， 
）上的函数f（x），f′（x）是它的导函数，且恒有f（x）＜f′（x）tanx成立，则（ ）
A.
f（ 
）＞ 
f（ 
）
B.f（1）＜2f（ 
）sin1
C.f（ ）＞f（ ）
D. f（ ）＜f（ ）
【答案】D
【解析】解：因为x∈（0， 
），所以sinx＞0，cosx＞0．
由f（x）＜f′（x）tanx，得f（x）cosx＜f′（x）sinx．
即f′（x）sinx﹣f（x）cosx＞0．
令g（x）= 
x∈（0， ），则 
．
所以函数g（x）= 在x∈（0， ）上为增函数，
则 
，即 
，所以 
，
即 
．
故选D．
【考点精析】关于本题考查的基本求导法则，需要了解若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导才能得出正确答案．
练习册系列答案
相关题目
