题目内容
已知无穷数列![]() 中,
中,![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列;
的等差数列;![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列![]() ,并对任意
,并对任意![]() ,均有
,均有![]() 成立,
成立,
(Ⅰ)当![]() 时,求
时,求![]() ;
;
(Ⅱ)若![]() ,试求
,试求![]() 的值;
的值;
(Ⅲ)判断是否存在![]() ,使
,使![]() 成立,若存在,求出
成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)![]() ;所以
;所以![]() (2分)
(2分)
![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列的第6项,所以
为公比的等比数列的第6项,所以![]() (4分)
(4分)
(2)![]() ,所以
,所以![]() (5分)
(5分)
因为![]() ,所以
,所以![]() ,其中
,其中![]() (6分)
(6分)
![]() ,
,
当![]() 时,
时,![]() ,成立。当
,成立。当![]() 时,
时,![]() ,成立;当
,成立;当![]() 时,
时,![]() 成立(9分)
成立(9分)
当![]() 时,
时,![]() ;所以
;所以![]() 可取9、15、45 (10分)
可取9、15、45 (10分)
(3)
 (12分)
(12分)
![]()
![]()
设![]() ,
,![]() (14分)
(14分)
![]() ;
; ![]() ,对称轴
,对称轴![]() ,所以
,所以![]() 在
在![]() 时取最大
时取最大
` ![]()
因为1922>1920,所以不存在这样的![]() (16分)
(16分)

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
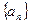 中,
中, 是首项为
是首项为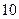 ,公差为
,公差为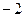 的等差数列;
的等差数列;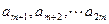 是首项为
是首项为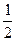 ,公比为
,公比为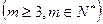 ,并对任意
,并对任意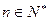 ,均有
,均有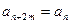 成立,(1)当
成立,(1)当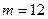 时,求
时,求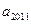 ; (2)若
; (2)若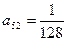 ,试求
,试求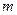 的值;(3)判断是否存在
的值;(3)判断是否存在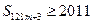 成立,若存在,求出
成立,若存在,求出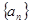 中,
中,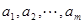 是首项为
是首项为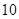 ,公差为
,公差为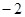 的等差数列;
的等差数列;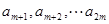 是首项为
是首项为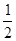 ,公比为
,公比为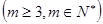 ,并对任意
,并对任意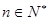 ,均有
,均有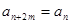 成立,(1)当
成立,(1)当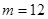 时,求
时,求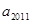 ; (2)若
; (2)若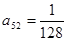 ,试求
,试求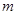 的值;(3)判断是否存在
的值;(3)判断是否存在 成立,若存在,求出
成立,若存在,求出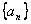 中,
中,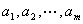 是首项为
是首项为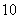 ,公差为
,公差为 的等差数列;
的等差数列; 是首项为
是首项为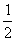 ,公比为
,公比为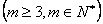 ,并对任意
,并对任意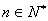 ,均有
,均有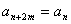 成立,
成立,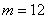 时,求
时,求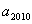 ;
; 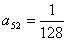 ,试求
,试求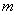 的值;
的值;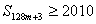 成立,若存在,求出
成立,若存在,求出