Question

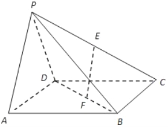
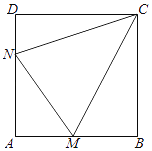
【题目】如图所示，某村积极开展“美丽乡村生态家园”建设，现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园，给村民休闲健身提供去处．点M，N分别在边AB，AD上． （Ⅰ）当点M，N分别是边AB，AD的中点时，求∠MCN的余弦值；

（Ⅱ）由于村建规划及保护生态环境的需要，要求△AMN的周长为2千米，请探究∠MCN是否为定值，若是，求出此定值，若不是，请说明理由．

Answer 1

【答案】（1）；（2）见解析.

【解析】试题分析：（Ⅰ）设∠DCN=∠BCM=θ，当点M，N分别是边AB，AD的中点时,在直角三角形中可得sinθ= ，cosθ= ，然后利用cos∠MCN=cos（ ﹣2θ）求解；

（Ⅱ）设∠BCM=α，∠DCN=β，探究α+β是否为定值即可。设AM=x，AN=y，则BM=1﹣x，DN=1﹣y，可得tanα=1﹣x，tanβ=1﹣y，于是得tan（α+β）= ，再由

△AMN的周长为2千米得xy=2（x+y）﹣2，代入后可得tan（α+β）=1.故可得α+β= ，于是可得∠MCN为定值。

试题解析:

（Ⅰ）当点M，N分别是边AB，AD的中点时，设∠DCN=∠BCM=θ，则∠MCN= ﹣2θ，

由条件得CD=BC=1，DN=BM= ，CN=CM= ，

所以sinθ= ，cosθ= ，

所以cos∠MCN=cos（ ﹣2θ）=sin2θ=2sinθcosθ= ，

即∠MCN的余弦值是 ．

（Ⅱ）设∠BCM=α，∠DCN=β，AM=x，AN=y，则BM=1﹣x，DN=1﹣y，

在△CBM中，tanα=1﹣x，

在△CDN中，tanβ=1﹣y，

所以tan（α+β）= = = ，（*）

因为△AMN的周长为2千米，

所以x+y+ =2，

化简得xy=2（x+y）﹣2，

将上式代入（*）式，可得

tan（α+β）= = = =1，

又，

所以α+β= ，

所以∠MCN是定值，且∠MCN= ．