题目内容
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.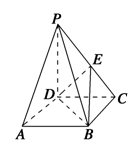
(1)证明:PA∥平面BDE;
(2)求二面角B-DE-C的余弦值.
(1)见解析(2)
解析

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
题目内容
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明:PA∥平面BDE;
(2)求二面角B-DE-C的余弦值.
(1)见解析(2)
解析

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案