题目内容
已知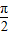 ≤θ≤π,且sin(θ-
≤θ≤π,且sin(θ-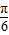 )=
)= ,则cosθ= .
,则cosθ= .
【答案】分析:由θ的范围求出θ-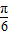 的范围,根据sin(θ-
的范围,根据sin(θ-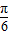 )=
)= ,利用特殊角的三角函数值求出θ的值,代入所求式子中即可求出cosθ的值.
,利用特殊角的三角函数值求出θ的值,代入所求式子中即可求出cosθ的值.
解答:解:∵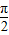 ≤θ≤π,∴
≤θ≤π,∴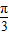 ≤θ-
≤θ-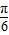 ≤
≤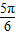 ,
,
又sin(θ-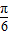 )=
)= ,
,
∴θ-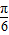 =
=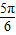 ,即θ=π,
,即θ=π,
则cosθ=cosπ=-1.
故答案为:-1
点评:此题考查了两角和与差的正弦函数公式,以及特殊角的三角函数值,牢记特殊角的三角函数值是解本题的关键.
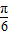 的范围,根据sin(θ-
的范围,根据sin(θ-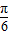 )=
)= ,利用特殊角的三角函数值求出θ的值,代入所求式子中即可求出cosθ的值.
,利用特殊角的三角函数值求出θ的值,代入所求式子中即可求出cosθ的值.解答:解:∵
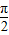 ≤θ≤π,∴
≤θ≤π,∴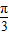 ≤θ-
≤θ-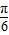 ≤
≤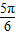 ,
,又sin(θ-
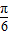 )=
)= ,
,∴θ-
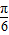 =
=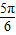 ,即θ=π,
,即θ=π,则cosθ=cosπ=-1.
故答案为:-1
点评:此题考查了两角和与差的正弦函数公式,以及特殊角的三角函数值,牢记特殊角的三角函数值是解本题的关键.

练习册系列答案
相关题目
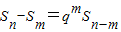 恒成立.
恒成立.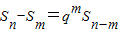 恒成立.
恒成立. 恒成立.
恒成立.