题目内容
设| a |
| 2 |
| b |
| π |
| 4 |
| π |
| 4 |
| a |
| a |
| b |
(Ⅰ)函数f(x)的最小正周期及最大值与最小值;
(Ⅱ)函数f(x)的单调递增区间.
分析:(Ⅰ)根据平面向量的数量积的运算法则列出f(x)的解析式,利用同角三角函数间的基本关系,二倍角的正弦、余弦函数公式化简后,再利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,由周期公式即可求出f(x)的最小正周期,根据正弦函数的值域即可得到f(x)的最大值和最小值;
(Ⅱ)由第一问确定出的f(x),根据正弦函数的单调递增区间,列出关于x的不等式,求出不等式的解集即可得到f(x)的单调递增区间.
(Ⅱ)由第一问确定出的f(x),根据正弦函数的单调递增区间,列出关于x的不等式,求出不等式的解集即可得到f(x)的单调递增区间.
解答:解:(Ⅰ)∵f(x)=
2+
•
=1+2(cosx+sinx)2+(1-2sin2(x+
))+2sin(x+
)cos(x+
)
=3+2sin2x+cos(2x+
)+sin(2x+
)
=3+sin2x+cos2x=3+
sin(2x+
)
∴f(x)的最小正周期T=
=π,f(x)max=3+
,f(x)min=3-
.
(Ⅱ)令2kπ-
≤2x+
≤2kπ+
(k∈Z)
解得kπ-
≤x≤kπ+
(k∈Z);
∴函数f(x)的单调递增区间为[kπ-
,kπ+
](k∈Z).
| a |
| a |
| b |
=1+2(cosx+sinx)2+(1-2sin2(x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=3+2sin2x+cos(2x+
| π |
| 2 |
| π |
| 2 |
=3+sin2x+cos2x=3+
| 2 |
| π |
| 4 |
∴f(x)的最小正周期T=
| 2π |
| 2 |
| 2 |
| 2 |
(Ⅱ)令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得kπ-
| 3π |
| 8 |
| π |
| 8 |
∴函数f(x)的单调递增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
点评:此题考查了平面向量的数量积的运算,三角函数的周期及其求法,三角函数的最值,以及正弦函数的单调性.利用平面向量的数量积的运算法则及三角函数的恒等变换确定出f(x)的解析式是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (2010•上饶二模)如图,设三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,三个侧面与底面所成的二面角O-AB-C,O-BC-A,O-CA-B分别等于α1,α2,α3.记△OAB,△OBC,△OCA,△ABC的面积分别为S1,S2,S3,S,则下列四个命题:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,则∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分别是30°,45°,60°.
(2010•上饶二模)如图,设三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,三个侧面与底面所成的二面角O-AB-C,O-BC-A,O-CA-B分别等于α1,α2,α3.记△OAB,△OBC,△OCA,△ABC的面积分别为S1,S2,S3,S,则下列四个命题:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,则∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分别是30°,45°,60°.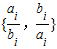 ≠min
≠min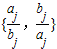 (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( )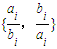 ≠min
≠min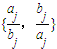 (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( )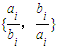 ≠min
≠min (min{x,y}表示两个数x、y中的较小者).则k的最大值是( )
(min{x,y}表示两个数x、y中的较小者).则k的最大值是( )