题目内容
在实数的原有运算法则中,定义新运算a?b=a-2b,则1≤m≤2是|m?(1-m)|+|(1-m)?m|=1的
- A.充分而不必要条件
- B.充要条件
- C.必要而不充分条件
- D.既不充分也不必要条件
C
分析:要作出正确的选择,得先求出满足方程|m?(1-m)|+|(1-m)?m|=1的m的取值范围,运用新定义运算化简该方程,构造函数可分析得m的取值范围,再判断它与1≤m≤2的关系即可.
解答:由题意得|m-2(1-m)|+|(1-m)-2m|=1,即|3m-2|+|1-3m|=1,
∴ ,令
,令 ,
,
则 ,
,
于是m的取值范围为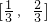 .而
.而 ,
,
故选C.
点评:本题的难点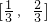 的求得,我们从函数的角度看出了满足方程|m?(1-m)|+|(1-m)?m|=1的m的取值范围,从而快速的解决问题.
的求得,我们从函数的角度看出了满足方程|m?(1-m)|+|(1-m)?m|=1的m的取值范围,从而快速的解决问题.
分析:要作出正确的选择,得先求出满足方程|m?(1-m)|+|(1-m)?m|=1的m的取值范围,运用新定义运算化简该方程,构造函数可分析得m的取值范围,再判断它与1≤m≤2的关系即可.
解答:由题意得|m-2(1-m)|+|(1-m)-2m|=1,即|3m-2|+|1-3m|=1,
∴
 ,令
,令 ,
,则
 ,
,于是m的取值范围为
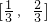 .而
.而 ,
,故选C.
点评:本题的难点
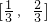 的求得,我们从函数的角度看出了满足方程|m?(1-m)|+|(1-m)?m|=1的m的取值范围,从而快速的解决问题.
的求得,我们从函数的角度看出了满足方程|m?(1-m)|+|(1-m)?m|=1的m的取值范围,从而快速的解决问题. 
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目