题目内容
已知函数 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若曲线 与
与 有三个不同的交点,求实数
有三个不同的交点,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ) 单调递增区间为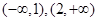 ,单调递减区间为
,单调递减区间为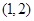 ;(Ⅱ)
;(Ⅱ) 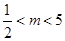 .
.
【解析】
试题分析:(Ⅰ)先对函数求导得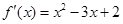 ,然后求出导函数的零点,讨论零点所分区间上导函数的正负,以此来判断函数的单调性,导数为正的区间是对应函数的递增区间,导数为负的区间是对应函数的递减区间;(Ⅱ)先化简
,然后求出导函数的零点,讨论零点所分区间上导函数的正负,以此来判断函数的单调性,导数为正的区间是对应函数的递增区间,导数为负的区间是对应函数的递减区间;(Ⅱ)先化简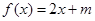 得到
得到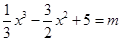 ,然后构造函数
,然后构造函数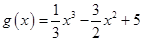 ,将问题转化为“函数
,将问题转化为“函数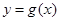 与
与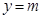 有三个公共点”.由数形结合的思想可知,当
有三个公共点”.由数形结合的思想可知,当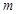 在函数
在函数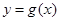 的两个极值点对应的函数值之间时,函数
的两个极值点对应的函数值之间时,函数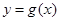 与
与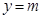 有三个公共点,那么只要利用函数
有三个公共点,那么只要利用函数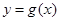 的导数找到此函数的两个极值即可.
的导数找到此函数的两个极值即可.
试题解析:(Ⅰ)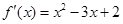 2分
2分
令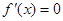 ,解得
,解得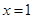 或
或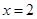 .
4分
.
4分
当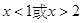 时,
时,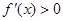 ;当
;当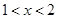 时,
时,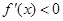
∴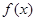 的单调递增区间为
的单调递增区间为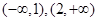 ,单调递减区间为
,单调递减区间为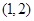 6分
6分
(Ⅱ)令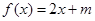 ,即
,即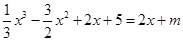
∴ 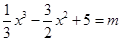
设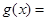
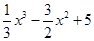 ,即考察函数
,即考察函数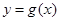 与
与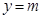 何时有三个公共点 8分
何时有三个公共点 8分
令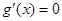 ,解得
,解得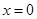 或
或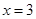 .
.
当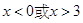 时,
时,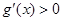
当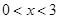 时,
时,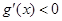
∴ 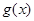 在
在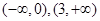 单调递增,在
单调递增,在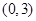 单调递减 9分
单调递减 9分
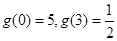 10分
10分
根据图象可得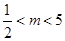 .
12分
.
12分
考点:1.函数的单调性与导数的关系;2.二次函数的图像与性质;3.解不等式;4.转化思想;5.数形结合思想;6.分类讨论思想

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.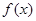 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求