题目内容
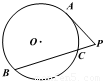
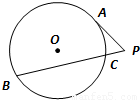
如图,⊙O的半径R=5,P是弦BC延长线上的一点,过P点作⊙O的切线,切点为A,若PC=1,PA=3,则圆心O到弦BC的距离是 .
【答案】分析:由已知中,⊙O的半径R=5,P是弦BC延长线上的一点,过P点作⊙O的切线,切点为A,若PC=1,PA=3,我们由切割线定理及求出PD的长,进而求出弦BC的长,然后根据半径弦长,弦心距,圆半径构成直角三角形,即可求出答案.
解答:解:由切割线定理得PA2=PC•PB,
从而PB=9,BC=8
则圆心O到弦BC的距离是
故答案为:3
点评:本题考查圆的切割线定理与垂径定理,属于中等题.其中根据切割线定理求出弦BC的长是解答本题的关键.
解答:解:由切割线定理得PA2=PC•PB,
从而PB=9,BC=8
则圆心O到弦BC的距离是

故答案为:3
点评:本题考查圆的切割线定理与垂径定理,属于中等题.其中根据切割线定理求出弦BC的长是解答本题的关键.

练习册系列答案
相关题目
 如图,⊙O的半径R=5,P是弦BC延长线上的一点,过P点作⊙O的切线,切点为A,若PC=1,PA=3,则圆心O到弦BC的距离是
如图,⊙O的半径R=5,P是弦BC延长线上的一点,过P点作⊙O的切线,切点为A,若PC=1,PA=3,则圆心O到弦BC的距离是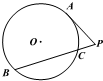 如图,⊙O的半径R=10,P是弦BC延长线上的一点,过点P作⊙O的切线,切点为A,若PC=2,PA=6,则圆心O到弦BC的距离是
如图,⊙O的半径R=10,P是弦BC延长线上的一点,过点P作⊙O的切线,切点为A,若PC=2,PA=6,则圆心O到弦BC的距离是