Question

15．从正方体的八个顶点中随机选择四个顶点，则以它们作为顶点的四面体是正四面体的概率等于（　　）

• A． $\frac{1}{35}$
• B． $\frac{1}{29}$
• C． $\frac{4}{35}$
• D． $\frac{4}{29}$

Answer 1

分析 根据题意，画出图形，结合图形求出对应的基本事件数，从而求出对应的概率．

解答 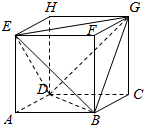解：如图所示，
从正方体的八个顶点中随机选择四个顶点，能构成四面体的基本事件数是
${C}_{8}^{4}$-6-6=70-12=58，
以这四个点为顶点的四面体是正四面体的基本事件数是2，
∴所求的概率为P=$\frac{2}{58}$=$\frac{1}{29}$．
故选：B．

点评 本题考查了古典概型的概率计算问题，解题时应仔细弄懂题意，以免出错，是基础题目．