题目内容
已知点M(x1,f(x1))是函数f(x)= ,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
(1)求切线l的方程;
(2)设l与x轴,y轴的交点分别为A、B,求△AOB周长的最小值.
 ,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
,x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.(1)求切线l的方程;
(2)设l与x轴,y轴的交点分别为A、B,求△AOB周长的最小值.
(1)y=- x+
x+ (2)△AOB周长的最小值是4+2
(2)△AOB周长的最小值是4+2
 x+
x+ (2)△AOB周长的最小值是4+2
(2)△AOB周长的最小值是4+2
(1)f′(x)=- ,∴k=f′(x1)=-
,∴k=f′(x1)=- .
.
∴切线方程为y- =-
=- (x-x1),
(x-x1),
即y=- x+
x+ .
.
(2)在y=- x+
x+ 中,令y=0得x=2x1,
中,令y=0得x=2x1,
∴A(2x1,0).令x=0,得y= ,∴B
,∴B .
.
∴△AOB的周长m=2x1+ +
+ .
.
∴m=2 ,x1∈(0,+∞).
,x1∈(0,+∞).
令t=x1+ ,∵x1∈(0,+∞),∴t≥2.
,∵x1∈(0,+∞),∴t≥2.
∴当t=2,即x1=1时,m最小=2(2+ ).
).
故△AOB周长的最小值是4+2 .
.
 ,∴k=f′(x1)=-
,∴k=f′(x1)=- .
.∴切线方程为y-
 =-
=- (x-x1),
(x-x1),即y=-
 x+
x+ .
.(2)在y=-
 x+
x+ 中,令y=0得x=2x1,
中,令y=0得x=2x1,∴A(2x1,0).令x=0,得y=
 ,∴B
,∴B .
.∴△AOB的周长m=2x1+
 +
+ .
.∴m=2
 ,x1∈(0,+∞).
,x1∈(0,+∞).令t=x1+
 ,∵x1∈(0,+∞),∴t≥2.
,∵x1∈(0,+∞),∴t≥2.∴当t=2,即x1=1时,m最小=2(2+
 ).
).故△AOB周长的最小值是4+2
 .
.
练习册系列答案
相关题目
 满足条件
满足条件 ,给出下列不等式:
,给出下列不等式: (2)
(2) (3)
(3) (4)
(4)

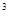 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2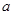 元/
元/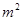 、
、 +
+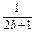 +
+ 的最小值.
的最小值.
 ,则下列不等式:①
,则下列不等式:①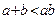 ;②
;② ;③
;③ ;④
;④ 中,正确的不等式有( )
中,正确的不等式有( ) ,则的整数部分是( )
,则的整数部分是( ) 在直线
在直线 上,则
上,则 的最小值是.
的最小值是.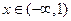 ,则函数
,则函数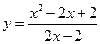 有( )
有( )
