题目内容
正方形ABCD边长为4,点E是边CD上的一点,将△AED沿AE折起到AED1的位置时,有平面ACD1⊥平面ABCE,并且BD1⊥CD1.(1)判断并证明E点的具体位置;
(2)求点D1到平面ABCE的距离.
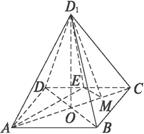
解:(1)连接AC、BD交于点O,再连结DD1,由BD⊥AC,且平面ACD1⊥平面ABCE于AC,
∴BD⊥平面ACD1,故CD1⊥BD,
又CD1⊥BD1,∴CD1⊥平面BDD1,即得CD1⊥DD1,
在Rt△CDD1中,由于ED=ED1,∴∠EDD1=∠ED1D,
则∠ECD1=90°-∠EDD1=90°-∠ED1D=∠ED1C,∴EC=ED1=ED,
即E点为边CD的中点.
(2)取OC的中点M,连结D1M、EM,则EM∥BD,得EM⊥平面ACD1,即∠EMD1=90°.
又因为D1E=2,EM=![]() ,则D1M=
,则D1M=![]() ,又AD1⊥EM,且AD⊥DE,∴AD1⊥D1E.
,又AD1⊥EM,且AD⊥DE,∴AD1⊥D1E.
∴AD1⊥平面EMD1,则AD1⊥D1M,
在Rt△AM D1中,A D1=4,AM=![]() , D1M=
, D1M=![]() ,过D1作D1H⊥AM于H点,则D1H⊥平面ABCE,
,过D1作D1H⊥AM于H点,则D1H⊥平面ABCE,
由于D1H=AD1 ·D1M/AM=(![]() )/(
)/(![]() )=4/3,
)=4/3,
此即得点D1到平面ABCE的距离.

练习册系列答案
相关题目
已知正方形ABCD边长为a,将△ABD沿正方形的对角线BD所在的直线进行翻转,在翻转过程中,说法不正确的是( )
| A、将△ABD沿BD翻转到任意位置时,直线AC与直线BD都垂直 | ||||
| B、当平面ABD垂直于平面BCD时,此时∠ACD=60° | ||||
C、沿BD翻转到某个位置时,使得三棱锥A-BCD体积最大值是
| ||||
| D、沿BD翻转到任意位置时,三直线“AB与CD”,“AD与BC”,“AC与BD”均不垂直 |
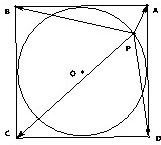 如图,正方形ABCD边长为2,内切圆为⊙O,点P是⊙O上任意一点.
如图,正方形ABCD边长为2,内切圆为⊙O,点P是⊙O上任意一点.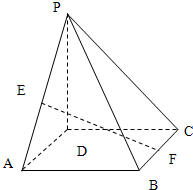 已知四棱锥P-ABCD中,PD⊥平面ABCD,正方形ABCD边长为2,PD=2,E,F分别是PA、BC的中点
已知四棱锥P-ABCD中,PD⊥平面ABCD,正方形ABCD边长为2,PD=2,E,F分别是PA、BC的中点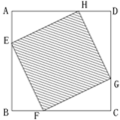 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )